ATN座標

ATN座標とは、XY座標の変形です。XY座標の場合には、X軸とY軸があり、それらが直角に交わることにより、平面上の点を(x,y)で表すことが出来るようになります。方程式も、軌跡を考えることでXY座標上でその形を描くことができるようになります。ATN座標も、基本的にXY座標と同じです。

ATN座標の場合は、XY軸の単位の取り方が、1,2,3、ではなく、atn(n)を基準にします。つまり、XY座標での(x,y)は(atn(x),atn(y)) となります。pa (pa=pi/2=1.570796327) と定義すると、(pa,0) がX軸上の無限大を示し、(0,pa)はY軸上の無限大です。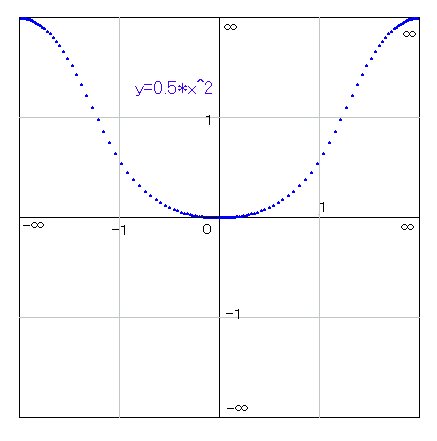



たとえば、0.5*x^2=y のグラフを描いてみましょう。XY座標であれば、いわゆる放物線になりますが、ATN座標では、右図のようになります。XY座標とATN座標は完全に一対一対応しているので、実質的に同じであり、数学的に新しいものを付け加えることはありません。しかし、無限を視覚的に捉えやすくしてくれるので、Σn^r や、n! を考えるときに大変便利です。

直感的には、このATN座標はもっと有意義な用いられ方があると思うのですが、その点については、今後研究してゆくつもりです。当面、今まで登場した方程式や級数の形を確認して、その図形と同型の方程式を求めたり、逆関数を求めたりして、ATN座標の有用性を確認してみようと思います。


まず、ゼータ関数のATN座標での軌跡を書いてみました。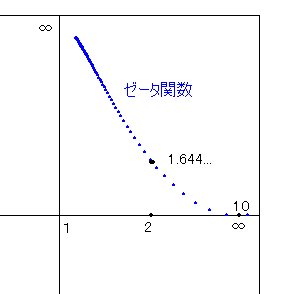

Σ1/n^r = 1 + 1/2^r + 1/3^r + 1/4^r + 1/5^r + . . . . .
ですから、だいたいのところを計算すると次のような数値になっています。

k(1.01) = 144.769
k(1.1) = 14.932
k(1.5) = 3.414
k(2) = 1.644
k(5) = 1.0369
k(10) = 1.000994

これをXY座標で表すこともできますが、比べてみると、ATN座標のほうが見やすいことがよく判ります。


　　


ゼータ関数の逆関数を求めてみました。これについては別ページで説明します。



1/f(x)を求めてみる

f(x)=Σ1/n^r 　（r>1)　としたとき、g(x)=1/f(x) なる式があるはずです。これを求めてみましょう。
（詳細説明）




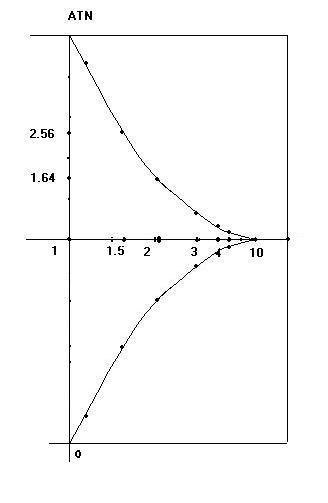
1/f(x)を移動させてみる

元の関数 f(x)=Σ1/n^r 　（r>1)　として、下図のような新しいf(x)を作り、その式を求めてみると、項数に面白い法則があることを発見しました。
（詳細説明）




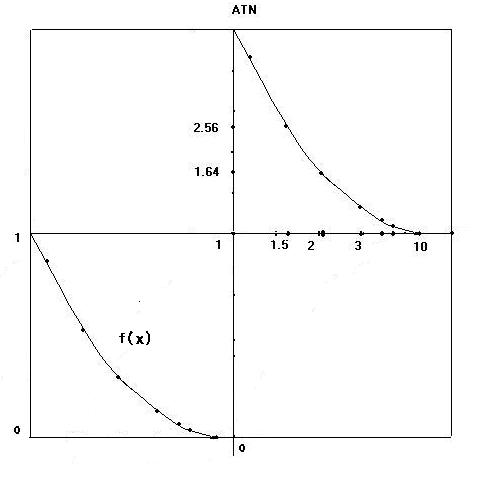
f(x)を移動させてみます

f(x)=Σ1/n^r 　（r>1)　として、これをATN座標の0と1の間に置いてみます。ATN座標で見ると、形はΣ1/n^rとまったく同じですが、XY座標ではまったく違った形に見えます。この式の項数は大変面白い変化をします。法則があると思うのですが、かなり膨大な計算をしても、確たることは言えません。おそらくあるだろうというのがいまのところの結論です。
（詳細説明）

表紙に戻る　　前のページへ　　次のページへ