逆関数

　　　　　　　　　　階乗の逆関数の解説はこのページの後半にあります。



逆関数（inverse function）というのはいった何だろうと、初めはとまどいました。y=f(x)において、x=g(y)を求めることであることは判るのですが、それがどういうものなのかイメージがつかめませんでした。y=1/(x+1)の逆関数が、y=(1-x)/x であるのは簡単に求められますが、y=x^3+3*x^2-2*x+4 などの逆関数は簡単に求められそうもありません。あまり話題にしても仕方のないテーマなのかと感じていたのですが、「 e^xの逆関数がlog(x)である 」と聞いて、少し興味を持ちました。複雑な関数の中にも逆関数という概念が当てはまる場合があるのですね。

少し興味を持って調べてみると、tan(x)の逆関数がarctan(x)であるとか、sin(x)の逆関数をsin＾-1(x)と書き表すとか、いろいろ教えられました。それはそれで納得しましたが、それ以上の関心が呼び覚まされることはなく、長らく無関心でいました。ところが、ATN座標というテーマを研究していたところ、逆関数について、私にとって新しい視点が与えられました。

y=f(x)をx=g(y)にするという説明も良いのですが、それだとx=g(y)を求められない場合が多いので、イメージが掴みずらく、取り上げようという意欲が湧いてきません。ところがATN座標を使って考えると、逆関数の意味が簡単に理解できるので、研究してみようという気になります。「意欲が湧く」という点は凄く大切ではないでしょうか。何事も意欲が湧く方向からアプローチしてゆけば道が開けてきます。

もっとも、意欲には個人差があるので、私の場合は意欲が湧いても、他の人には面白くも何ともないということもあるでしょう。それはそれで仕方ありません。例によって、ここではあくまでも私個人の意欲の湧いたテーマだけを追求していきます。



■　　　　　　ATN座標とは


ATN座標という言い方は私の開発したものなので、説明が必要でしょう。ATN座標とは ｘｙ座標のｘ軸をarctan(x) に、ｙ軸を arctan(y) に変換して表示する座標図です。たとえば、(10,3) という点はｘｙ座標では右図の青点の場所を意味します。ATN座標では無限大が pi/2 になります。arctan(∞)=1.57079... ということです。pa=pi/2 とすると、arctan(1)=pa/2、arctan(0)=0 となります。x=10 は arctan(x)=1.471127... なので、それをｘｙ座標に合わせるために pa で割ります。0.93654... を右図のｘｙ座標に合わせるために１０倍すると　9.3654... となります。y軸については、y=3 を arctan(3)=1.2490... として、これを　pa で割ります。0.79516...　を右図のｘｙ座標に合わせるために４倍します。その結果が　3.1806... です。

ｘｙ座標で (1, 0.5) の場所に青点を打ちます。ATN座標では　arctan(1)=0.7853..., arctan(0.5)=0.4636...　です。ここに赤点を打ちます。


ATN座標とｘｙ座標は基本的には同じもので、違いは縮尺だけですが、ATN座標では無限を有限の点で表示できるので、関数の無限大での形を目で見ることができます。

逆関数はｘｙ座標では x=y の線に対称な形の関数となります。ATN座標も同じ構造です。ただし、ATN座標では無限大の形も含めて対称であることが図示されるので、逆関数とはどういうものかを視覚的にとらえることができます。これにより、逆関数の式を求めてみようという意欲が湧いてくることになるのです。




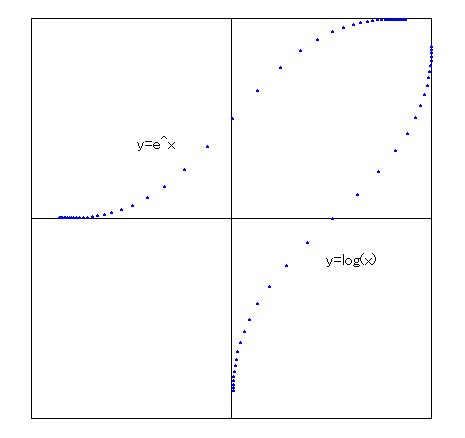
具体例として　e^x と log(x) のグラフを描いてみました。e^x と log(x) は逆関数の関係にあります。

このグラフを見れば判るように、e^x と log(x)　は、y=x 線上で対称となっています。どのような関数であれ、ATN座標で表示した後、その形と対称の図形を示す関数を求めることが逆関数を求めることになります。



Y=X^2の逆関数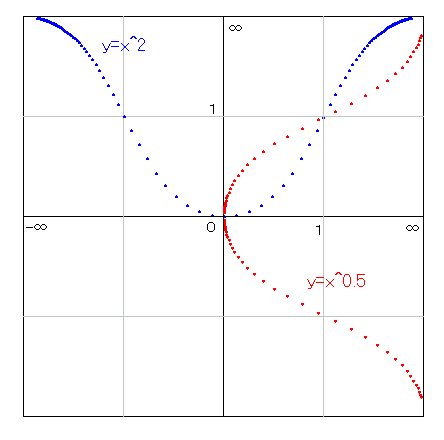


y=x^2 は最も初歩的関数の一つで、放物線と呼ばれることもあります。
これをATN座標で書くと放物線ではなくなりますが、非常に綺麗な線であることに変わりありません。
この式の逆関数は、ATN座標に表示しなくても判ります。つまり、
y=√x です。この線を赤色で示してみると、両者が y=x 線上で綺麗に対称となっていることが判ります。

どのような y=f(x) でも、ATN座標に書くことが出来るなら、y=x線に対して対称の図形が必ずひとつ存在するので、逆関数もかならずひとつだけ存在することが判ります。ただし、その関数を通常の数式で書き表すことが出来るかどうかは別問題です。
おそらく、すべて可能だろうとは思いますが、中には難しいのもあるかもしれません。そこで、試しに、いくつかの関数の逆関数を求めてみました。



ゼータ関数の逆関数


それでは手始めにゼータ関数の逆関数を求めてみました。
y=1+1/2^x+1/3^x+1/4^x+1/5^x ....... ですから、逆関数を求めると言っても、簡単ではないという感じがします。しかし、ATN座標に書いて、y=x軸に対称である図形と考えると、どういう形かすぐに思いつきます。あとは、その図形を表す関数を求めればよいということになります。判ってしまうと求められそうな気がするものです。そして、求められそうという気持ちが解決方法を思いつくエネルギーになります。数学研究も動機付けが重要なのです。

さて、実際に求めるやり方は簡単ですが、時間がかかります。ここでは、最初ですから、初歩的なところから説明しておきます。

まず、y=f(x) で、x=2, 4, 8, 16, 64.... と順次代入して、yの値を求めておきます。すると、近似的に x=g(y) となるような式を思いつくはずです。

実際にと言っても、本当に計算するのは大変です。すでに、su(n)の計算は出来ているし、ベルヌーイ数も1000まで計算してあるので、suの公式を使って、f(x) を計算することが可能です。つまり、
su(x)=2/(2pi)^x* { 1+1/2^x+1/3^x+1/4^x+..... }　ですから、f(x)=su(x)*(2pi)^x/2 となります。これなら時間がかかりません。

まず、xが大きくなるとyは1に近づくので、y-1 とします。その次は、急激に0に近づくので、x=a*log(1/(y-1))と置いて、多桁計算ソフトを使ってaを計算してみました。すると、a=3.321928095 となり、1/log(2) であることが判りました。次に、p=1/(y-1) と書くことにして、x-log(p)/log(2)=p^a と置いて、このaを計算したところ、a=0.584.... となり、なかなか確定してくれません。しかし、収束することは間違いなさそうなので、いろいろ工夫したところ、a=log(2/3)/log(2) である可能性が大きいと見えてきました。これを前提にすると、pの項数がlog(e)/log(2)に収束してくれます。

さて、その次ですが、log(e)/log(2)/pとなり、次をp^bとおいてbを求めたところ、b=-1.169...あたりに収束しました。これは、先のlog(2/3)/log(2)の倍に近いので、関連があるのではないでしょうか。

この先を求めるのは大変ですが、時間さえかければさらに詳しい式の内容を掴むことが出来るはずです。
一応、このあたりまでを纏めて、x,yを置き換えて表示しておきます。

p=1/(x-1)として、y = log(p) / log(2) + p^{(log(2/3)/log(2)} + log(e)/(log(2)*p) + ........ となり、これがゼータ関数の逆関数と言うことになります。



y=x^3+3x^2-2x+4 の逆関数


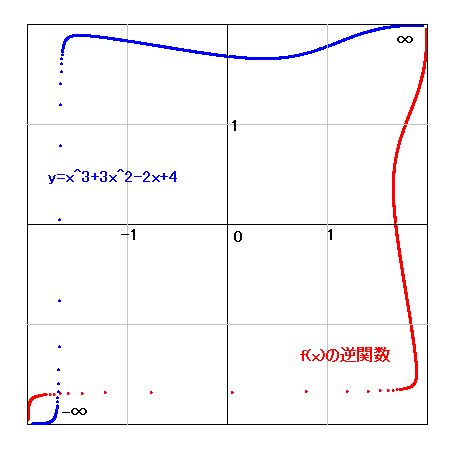
ゼータ関数は取っつきにくいと言う人のために、初歩的関数の中では難しそうに思える　y = x^3 + 3x^2 - 2x + 4 を取り上げてみようと思います。この関数になったのはまったくの偶然、つまり適当に選んだもので、形が綺麗だとか、有益というわけではありません。これにも逆関数があるということを示すことにより、ATN座標のわかりやすさを説明することにします。

この関数はマイナスになると急激に減少するので、グラフに書きにくいのですが、間隔を小さくしたところ、ようやくグラフらしくなりました。やや線が太めなのはそのためです。

赤い線が逆関数で、その式は、x=4 でy=0 で、xが増加すると急激に大きくなります。どのような関数になっているかは多桁計算ソフトを使って実際に計算してみました。当然、y=f(x) よりは小さい値ですから、おそらく　y=x^(1/3) あたりになるのではと推測できます。事実その通りになっていました。その先についても計算してみると次のようになりました。綺麗に表現するために、 p=x^(1/3) と置いておきます。　y= p-1+5/3p-8/3p^2+4/9p^4 - 701/81p^5 + ...... となっています。

式の求め方は、元の関数 y=f(x) を実際に計算してみて、その x を yで表現できる式を探すと言うことです。特に難しいと思わないので、これ以上説明しませんが、y=3x^3 とか、y=x^2+5 などの簡単な式の逆関数を求めてみて、そのやり方を参考にすればすぐに判ります。多桁計算ソフトの使い方については別途説明してあります。（現在、ソフトを修正中なので、できあがり次第、再度解説を載せることにします。使い方としては以前のソフトとほとんど同じです。）


Σ(1/n)の逆関数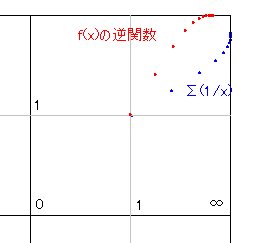

Σ(1/x)は、無限級数ですから、逆関数といってもすぐにはピンときませんが、ATN座標に書いてみると、意外と簡単にイメージすることが出来ます。多桁計算ソフトを使い、ｘが充分に大きいところで、ｘをｙで表現してみると、項数が有理数になって現れました。

p=e^(x-eu) とします。eu=0.57721566。すると、
y = p - 1/2 - 1/(24p) + 11/(5760*p^3) - 1/(180*p^4)
- 4741/(580608*p^5) + .....
と書くことが出来ます。計算を続ければ、項数はいくらでも確定させることが出来ます。何か法則があると良いのですが、今のところ見つかりません。






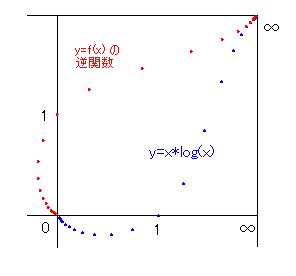
y=x*log(x) の逆関数

少し難しそうな問題にもチャレンジしてみます。y=x*log(x)の逆関数などはどうでしょうか。実際、計算してみたところ、なかなかうまくいきませんでした。いろいろ苦労した結果、以下の式を求めることが出来ました。

p=log(log(x))/{ log(x)-log(log(x)) } と置きます。すると逆関数は、
y = x/log(x) * { 1+ p(1-g(x)) }　となります。このg(x)は、1/x^rよりも大きくて1/log(x)^rよりは小さい数になりますが、どのような表現になるのか現在研究中です。はたしてそのような数を表記できるのでしょうか・・・。

x<1の時、log(log(x))が成り立ちませんが、式表現としてはこんなところです。



＜２０２２・７・９　追加＞

x*log(x) の逆関数は x^x のところで説明した　lac(x) と密接な関係があります。便宜上、x*ln(x)という自然対数で説明させてください。lac(x)はlog(x)を使って計算しますが、lec(x) は ln(x) で計算します。計算方法は同じですが、答えは違ってきます。

lec(x)の計算方法は、以前 lac03(x) として説明したものと同じです。f1(x)=x/ln(x) として、f2(x)=x/ln(f1(x))、3(x)=x/ln(f2(x)) 、f4(x)=x/ln(f3(x))、・・・　と計算をつづけたときの極限値が　lec(x) となります。

x*ln(x) の逆関数はこの lec(x) となります。多桁計算プログラムの中の　Tk3.javaに Tk3.lec(a,b,p3) という名前で入れてあります。a,b は自分で選べる関数の名前で、p3 は計算深度（繰り返しの数）です。 int数なので、自分で指定してください。精度を超えて零になるなら自動で停止するので、数を増やしても問題ありません。

たとえば、x=5 のときは　x*ln(x) = 8.0471895　で、lec(8.047...)=5　となります。5^5=3125 ですが、e^(x*ln(x)=3125 となります。







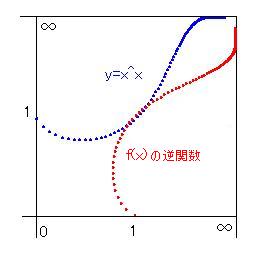
y=x^x の逆関数

x^x は重要な関数ですが、逆関数を求めることは容易ではありませんでした。もしかすると普通の式では表せないかもしれません。今のところ、便宜上新しい関数を定義して、それで表現しておきます。

新しい関数は lac(x) と名付けて、以下のように定義します。
f1(x)=x/log(x) として、f2(x)=x/log(f1(x)) とします。f3(x)=x/log(f2(x)) 、f4(x)=x/log(f3(x)) となるので、順次計算が可能となります。この極限値が lac(x) です。

たとえば、lac(30) = 22.2622954..... であり、lac(5) = 6.270919.... 、lac(1.385) = 2.9433878.... となります。

x<1.38 の範囲で計算不能になりますが、値が存在しないわけではありません。たとえば lac(1) = 2.506184.... であることは y=xlog(x) の図から計算できます。

lac(1)^lac(1) = 9.999997206.... となっていることから判るように、lac(x)^lac(x) = 10^x という関係にあります。

このlac(x)を使ってx^xの逆関数を表示すると、y=lac(log(x)) となります。


ln(x) を軸として考えるときの関数を　lac03(x) とします。この場合は　f2(x)=x/ln(f1(x)) というやり方で計算します。その極限値が　lac03(x) となります。この場合、 lac03(x)^lac03(x) = e^x　という関係になります。




(x/2)^x の逆関数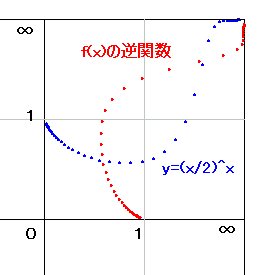


x!の逆関数は、なかなか確定しないので、その前に (x/2)^x の逆関数を求めてみることにしました。logではなかなか確定しないので、lacを使ってみたところ、簡単に確定してくれました。
y=2*lac(log(x)/2) が逆関数です。

(x/3)^xの逆関数は、y=3*lac(log(x)/3)となり、(x/4)^xの逆関数はy=4*lac(log(x)/4)となります。結構綺麗に並んでいます。




n! 階乗の逆関数


n! 階乗の逆関数の図はすぐに書くことが出来ます。しかし、それを式に表そうとすると、簡単ではありません。

巨大な数を扱うので、今までのプログラムを変更してgigaプログラムを作りました。これで計算したところ、結構複雑な式が出てきました。綺麗な式にならなかったので、面白くありませんが、おそらく未発見の式だと思うので、ここに書いておきます。

P=e*lac((log(x)/e) 、また、L=log(√2pi) = 0.3990899342 、ei = log(e) = 0.4342944819 と表記することにします。

以下は、以前公表したものですが、赤字部分は間違っていたようなので撤回します。正しくは、その後の解説を参照してください。

すると、逆関数は、P - 1/2 - L/log(P) + ei/24log(x) -ei^2/24log(x)log(P) -ei*L^2/2log(x)log(P)^2 +ei^2*L^2/2log(x)log(P)^3 +.....　となります。


もう少し綺麗に書くやり方があるのではないかと思うのですが、今のところこの程度です。


＜2022/05/31 追加＞
久しぶりに階乗の逆関数の続きを計算してみました。なんと別の式になってしまいました。似てはいますが、少し・・・というか、かなり違います。

新しく求めた式は、P=e*lac((log(x)/e) 、また、L=ln(√2pi) = 0.9189385334　とすると、

P - 1/2 - L/ln(P) + 1/24P/ln(P) - L^2/2P/ln(P)^3 + L/24P^2/ln(P)^2 + L/24P^2/ln(P)^3 - L^3/6P^2/ln(P)^4 - L^3/2P^2/ln(P)^5 - 7/2880P^3/ln(P)

となりました。

x=3628800 として、この式で計算すると答えが　10.002431...　となり、綺麗に収束してくれません。おそらく、ベルヌーイ数のように振動するのだろうと思いますが、どこかに計算間違いか、プログラムミスがあるのかもしれません。上記の式は何度か再計算しましたが、間違いはなさそうです。式は　x→∞　で成り立つという前提で計算しているので、ｘが小さいときは誤差が生じるのかもしれません。しかし、この答えのズレは誤差と言うものではないので、さらなる検討が必要です。（階乗の公式を使って逆関数を計算しています。階乗の公式にはベルヌーイ数が使われているのである程度しか確定しません。それが原因かもしれません。）

逆関数を直接計算するプログラムを　Tk3.java の中に　Tk3.kaijoo_gyaku(a,c); という名で入れてあるので、関心のある人は使うことができます。「多桁計算」のＨＰからダウンロードできます。







■　　　　　　x!　階乗の逆関数の求め方
＜２０２２・０６・１４＞



階乗の逆関数は簡単には求められないので、その分析方法を書き留めておきます。

巨大数を扱うための giga計算プログラムを作りました。これにより、x=10^200 でも　x^x を計算することができます。それを使って逆関数を求めた結果が前章の赤字で書いた式になりました。計算は可能でも、精度が足りないので、間違った式になってしまいました。

今回、より広い視野から階乗をとらえ、階乗の公式の部品をひとつひとつ別々に分析することにし、最後にそれを総合するやり方にしてみました。

階乗の公式とは　　　(x/e)^x * √(2pi * x) * e^mo(x) というものです。

　　　mo(x) = 1/12x - 1/360x^3 + 1/1260x^5 ...
　　　e^mo(x) = 1 + 1/12x + 1/288x^2 - 139/51840x^3 - 571/2488320x^4 ....

式の解説については、「実数値での階乗計算方法」などのページを参照してください。

階乗の公式は　(x/e)^x 　と　√(2pix)　と　e^mo(x) 　の部分からできています。(x/e)^x が巨大数になる部分で、これが全体の値の核となります。これに他のふたつがぶら下がっている構造をしています。　　　




■　　　　　　(x/e)^x の逆関数


(x/2)^x などの逆関数については、このページの前半で解説してあります。2*lac(log(x)/2) となります。この２の部分を　e 　に置き換えると　(x/e)^x の逆関数になります。e*lac(log(x)/e) ということです。lac(x) については、このページの前半を参照してください。10^x=y とすると、y = lac(x)^lac(x) という関係です。





■　　　　　　(x/e)^x * x の逆関数


(x/e)^x に　√(2pix) を掛けた式の逆関数は複雑なので、まずは　x　を掛けた式の逆関数を求めます。

y = (x/e)^x * x　とおいて、yを変数とする関数が逆関数になります。便宜上、y　を新しい関数の x と表記します。このｘは　(x/e)^x の　ｘ　ではなく、逆関数の変数としてのｘですので、ご注意ください。つまり、e*lac(log(y)/e) を　e*lac(log(x)/e) と表記するということです。

(x/e)^x * x　の逆関数は　e*lac(log(x)/e) から変化した形になるはずで、それがどうなるかを調べます。P = e*lac(log(x)/e) とします。その結果、次の式を得ることができました。


P - 1 + 1/2P/ln(P) + 1/3P^2/ln(P) + 1/4P^3/ln(P) - 1/4P^3/ln(P)^2 - 1/8P^3/ln(P)^3 + 1/5P^4/ln(P) - 1/2P^4/ln(P)^2 + 1/6P^4/ln(P)^3 - 1/6P^5/ln(P) + 13/18P^5/ln(P)^2 + ....


式の構造ははっきりしました。つまり、1/P/ln(P) が基本であることです。すべて　P^r と　ln(P)^r の組み合わせです。式が長いので、P^r ごとに纏めて表示すると、

P のときが　　1/2P/ln(P)、
P^2 のときが　　1/3P^2/ln(P) + 0/P^2/ln(P)^2、
P^3 のときが　　1/4P^3/ln(P) - 1/4P^3/ln(P)^2 - 1/8P^3/ln(P)^3 　と並びます。

係数だけを取り出して並べると、

P　のとき　　1/2　
P^2　のとき　　1/3, 0　
P^3　のとき　　1/4, -1/4, -1/8　
P^4　のとき　　1/5, -1/2, -1/6, 0　
P^5　のとき　　1/6, -13/18, 5/72, 5/24, 1/16
P^6　のとき　　1/7, -11/12, 13/20, 13/24, 1/8, 0　
P^7　のとき　　1/8, -87/80, 763/480, 91/144. -3679/20160(?) , 　, 　

となります。法則はまだ見つかりません。



(x/e)^x * x^2　の逆関数は上記の式に２の累乗を掛けたものとなっています。

P - 2 + 4/2P/ln(P) + 8/3P^2/ln(P) + 16/2P^3/ln(P) - 16/2P^3/ln(P)^2 - 16/4P^3/ln(P)^3 + 32/5P^4/ln(P) - 32/2P^4/ln(P)^2 - 32/6P^4/ln(P)^3 + 64/6P^5/ln(P) - 64*13/18P^5/ln(P)^2 + ....


一般的に　r を使って表記すると　(x/e)^x * x^r 　の式は

P - r + r^2/2P/ln(P) + r^3/3P^2/ln(P) + r^4/4P^3/ln(P) - r^4/4P^3/ln(P)^2 - r^4/8P^3/ln(P)^3 - r^5/5P^4/ln(P) + r^5/2P^4/ln(P)^2 + r^5/6P^4/ln(P)^3 - r^6/6P^5/ln(P) + r^6*13/18P^5/ln(P)^2 + ...


つまり、(x/e)^x * x を研究すれば、(x/e)^x * x^r を研究したことになるということです。

階乗の公式では　r=0.5 となるので、上記の式に　r=0.5 を代入すると求められます。

P - 1/2 + 1/8P/ln(P) + 1/24P^2/ln(P) + 1/64P^3/ln(P) - 1/64P^3/ln(P)^2 - 1/128P^3/ln(P)^3 - 1/160P^4/ln(P) + 1/64P^4/ln(P)^2 + 1/192P^4/ln(P)^3 - 1/384P^5/ln(P) + 832/18P^5/ln(P)^2 + ...




■　　　　　　 (x/e)^x * e^mo(x) の逆関数


(x/e)^x に　e^mo(x) を掛けた式の逆関数を求めます。

P + 1/12P/ln(P) + 1/360P^3/ln(P) + 1/144P^3/ln(P)^2 - 1/144P^3/ln(P)^2 - 1/288P^3/ln(P)^3 +

という結果になります。さらに精度を上げるともっと詳しい式が見つかるでしょう。しかし、係数の法則はまだわかりません。




■　　　　　　 (x/e)^x * x * e^mo(x) の逆関数


x のあとに続かせると式が変化します。

逆関数を計算すると

P - 1 + 5/12P/ln(P) + 1/4P^2/ln(P) + 61/360P^3/ln(P) - 25/144P^3/ln(P)^2 - 25/288P^3/ln(P)^3 + 1/8P^4/ln(P) - 45/144P^4/ln(P)^2 - 5/48P^4/ln(P)^3 ...

(x/e)^x * e^mo(x) と似た数値になっていますが、法則はあるのでしょうか？






■　　　　　　(x/e)^x * a　の逆関数


(x/e)^x に数字を掛けただけの式で逆関数を求めてみます。結論から言うと、有理数化してくれないので、期待した結果にはなりませんでした。

a=2 とすると、 L=ln(2) と表記して、


P - L/ln(P) - L^2/2P/ln(P)^3 + α*L^3/P^2/ln(P)^4 + ???

α=-0.167209310 となりますが、今のところ有理数化しません。

a=3, 4, 5, ... としても　αの値はだいたい同じです。




■　　　　　　(x/e)^x * a * x　の逆関数


そこで、　x を加えて分析することにします。　(x/e)^x * a * x の逆関数を求めます。

a=2 とすると　　　P=e*lac((log(x)/e) 、L=ln(2) = 0.6931471、として、

P - 1 - L/ln(P) + 1/2P/ln(P) - L^2/2P/ln(P)^3 + 1/3P^2/ln(P) + L/2P^2/ln(P)^2 + L/2P^2/ln(P)^3 - L^3/6P^2/ln(P)^4 - L^3/2P^2/ln(P)^5 + 1/4P^3/ln(P) + 1/4P^3/ln(P)^2 2L/3P^3/ln(P)^2 ..

(x/e)^x * a　と整合性がない部分が現れます。(x/e)^x * x 　と同じ部分は良いとして、それ以外は　(x/e)^x * a と一致しているのかと思っていたのですが、P^2 の列を見ると、かなり違っています。a*x と　a では基本構造が変化するようです。



■　　　　　　(x/e)^x * a√x　の逆関数


ならば、　(x/e)^x * a√x の場合に同じ構造なのかを確認します。

a=2 とすると、

P - 1/2 - L/ln(P) + 1/8P/ln(P) - L^2/2P/ln(P)^3 + 1/24P^2/ln(P) + L/8P^2/ln(P)^2 + L/8P^2/ln(P)^3 - L^3/6P^2/ln(P)^4 - L^3/2P^2/ln(P)^5 + 1/64P^3/ln(P) ...

だいだい同じ法則です。しかし、細部において違いが発生しています。どう考えるべきでしょうか？




■　　　　　　(x/e)^x * √(2pi*x) の逆関数


ようやく階乗の公式に近くなってきました。　　(x/e)^x * √(2pi*x) を調べてみます。 L=ln(√2pi) = 0.9189385334

先に分析した式を総合したものであることが予想されます。

P - 1/2 - L/ln(P) + 1/8P/ln(P) - L^2/2P/ln(P)^3 + 1/24P^2/ln(P) + L/8P^2/ln(P)^2 + ...

表記としては先の式とまったく同じです。




■　　　　　　(x/e)^x * √(2pi*x) * e^mo(x)　の逆関数


(x/e)^x * √(2pi*x) に e^mo(x)　を掛けると階乗の公式になります。つまり、これが階乗の逆関数と言うことになります。先の　e^mo(x) の逆関数を参考にしつつ、この式の逆関数を計算してみましょう。

P - 1/2 - L/ln(P) + 1/24P/ln(P) - L^2/2P/ln(P)^3 + ????

？？？　　1/P^2/ln(P) の値が定まりません。０に向かっているように見えるので、1/P^2/ln(P)^2 を計算すると　0.0383　あたりになりますが、特定できません。e^mo(x) がなければ　1/24P^2/ln(P) になるのに、なぜ　値がないのか？




■　　　　　　(x/e)^x * e * x * (1+1/12x+1/288x^2)


反省を含めて、いろいろ検討した結果、一部の値が特定できないのは　L=ln(√2pi)　などの値と合計された数値が出てくるからだとわかりました。そこで、L = ln(e) = 1　 とおいて、係数のみを特定することにしました。


P - 1 - 1/ln(P) + 10/24P/ln(P) - 1/2P/ln(P)^3 + 10/24P^2/ln(P)^2 + 10/24P^2/ln(P)^3 - 1/6P^2/ln(P)^4 - 1/2P^2/ln(P)^5 + 1/6P^3/ln(P)

このやり方だと問題なく値が特定できます。




■　　　　　　(x/e)^x * e * √x * (1+1/12x+1/288x^2)


√x にしないといけません。

P - 1/2 - 1/ln(P) + 1/24P/ln(P) - 1/2P/ln(P)^3 + 1/24P^2/ln(P)^2 + 1/24P^2/ln(P)^3 - 1/6P^2/ln(P)^4 - 1/2P^2/ln(P)^5 + 7/2880(?)P^3/ln(P)

このやり方だと問題なく値が特定できます。




■　　　　　　(x/e)^x * √(2pix) * e^mo(x)


上記の式を前提に　L=ln(√(2pi)) として計算してみると、以下の結果になりました。


P - 1/2 - L/ln(P) + 1/24P/ln(P) - L^2/2P/ln(P)^3 + L/24P^2/ln(P)^2 + L/24P^2/ln(P)^3 - L^3/6P^2/ln(P)^4 - L^3/2P^2/ln(P)^5 - 7/2880P^3/ln(P)

これが階乗の公式の逆関数です。時間をかけるとさらに詳しい式が求められますが、疲れたので、このへんで止めておきます。








■　　　　　　ln(x!)　の逆関数
＜２０２２・０７・０４＞

ln(x!) = x*ln(x) - x + ln(x)/2 + ln(2pi)/2 + mo(x)　ですから、個別に逆関数を求めてゆきます。

まずは　x*ln(x)　ですが、これは　lac(x) と同じ操作で　log(x) のところを　ln(x) に変更します。lac(x) と区別して　lec(x) と表記することにします。x*ln(x) の逆関数は　lec(x) となります。

x*ln(x) - x + ln(x)/2 の逆関数は、P=lec(x)　とすると、

P + 1 + 1/ln(P) - 1/2ln(p)^3 + 1/6ln(P)^4 + 5/12ln(P)^5 - 11/30ln(P)^6 - 13/40ln(P)^7 ...　となります。


x*ln(x) + x の逆関数は、

P + 1 + 1/ln(P) + 2/ln(p)^2 + 9/2ln(P)^3 ...　となります。



x*ln(x) - 2x の逆関数は、

P + 1 + 2/ln(P) + 2/ln(p)^2 + 0/ln(P)^3 - 8/3ln(P)^4 - 2/ln(P)^5 + 18/5ln(P)^6 + 34/5ln(P)^7 ...　となります。


x*ln(x) -3x の逆関数は、

P + 1 + 3/ln(P) + 6/ln(p)^2 + 15/2ln(P)^3 + 3/2ln(P)^4 (?) ...　となります。


x*ln(x) -4x の逆関数は、

P + 1 + 4/ln(P) + 12/ln(p)^2 + 28/ln(P)^3 + 140/3ln(P)^4 (?) ...　となります。

以上をまとめると、x*ln(x) - a*x　の逆関数の　ln(P) の係数は　a　で、ln(P)^2 では a(a-1)、　ln(P)^3 は a(a-0.5)(a-2) 、ln(P)^4 は　a(a-0.306)(a-1.126)(a-2.9025) となります。有理数としても綺麗な有理数にならないので、綺麗な公式にならないかもしれません。

これを(1-a)(1-b)(1-c)=1/6 , 　2(2-a)(2-b)(2-c)=-8/3,　3(3-a)(3-b)(3-c)=3/2　とおくと、a+b+c=13/3, ab+bc+ac=9/2, abc=1　という結果になります。これは、根と級数の関係から　x^3-13/3x^2+9/2x-1=0 の解となっていることがわかります。たとえば、x=3 とすると、y=0.5 となり、0.5*3=1.5 で一致します。

これで　-5x 以降も計算可能となります。ただし、ln(P)^5 になると、基礎となる数字の計算が面倒なので、式を求めるのに時間がかかりそうなのと、法則性が見つかりにくそうなので、このへんで止めておきます。