リーマン仮説（リーマン予想）を納得する方法 ver 4

普通、証明というのは「事実上正しいと認定されていることを証明する」のではないでしょうか。三角形の内角の和が１８０度であることは、古代から多くの人により正しいと認められてきました。しかし、証明されたのは古典ギリシャ時代になってからのことです。証明は事実認識とは別で、まずは事実認識があり、それから証明が完成します。リーマン仮説の場合は、まだ「事実上正しい」と認定されているわけではないようで、反証の可能性を認める人がいます。それにも関わらず証明にトライすると言うことは、手順前後の誤りがあるとも言えます。まずはリーマン仮説が疑う余地のない正しい定理であることを認識して、その上で証明に取りかからなければなりません。ですから、「リーマン仮説が事実上正しい」ということを納得できるようにすることは、いまだ少しは意義のあることではないかと考えます。

以下の説明では、リーマン仮説が正しいことをいくつかの角度から説明してあります。証明ではないので、直感にたよるやり方を使っていますが、これでリーマン仮説の反証を見つけようという試みがいかに無意味であるかがわかっていただけることと思います。リーマン仮説を疑う余地はまったくありません。あとは、これをいかにして証明するかという問題が残るだけです。




■　　　　リーマンの零点を図示します。


まずは素朴に、リーマンの零点の場所を調べてみることにします。その結果を図示して、それがa=0.5とb=0上にしかないことがわかればよいはずです。

リーマン零点の計算方法は、別ページで説明してありますが、ここでその要点だけ再述しておきます。一般にはまだk(x)がリーマンの零点を求める式であることが認識されていないのですが、実際に計算してみれば誰でもこの式の正しさを認識することが出来ます。

k(x)はゼータ関数によって定義されます。つまり、
Σ1/n^r = k(r)-1/(r-1)/n^(r-1) + 1/2/n^r - r/12/n^(r+1) + 0 + r*(r+1)*(r+2)/6!/n^(r+3) + 0 + .....

この　k(r)　を複素数にしたものがリーマン・ゼータ関数となります。これを整理して表記すると、

k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }

zt(s,n)　と　ber(s,n)　は以下の式となります。

zt(s,n) = 1 + 1/2^s + 1/3^s + . . . + 1/n^s
ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

ということです。これについては第５の広場でさらに詳しく説明しているので、そちらを参照していただければと思います。

さて、このk(s)の式を使ってリーマンの零点を探してみます。具体的計算方法については、別ページ「リーマン仮説と零点の計算方法」を参照してください。

複素数a+biを複素平面と見なし、z1+z2i=k(a+bi)とすると、z1をZ軸とするXYZ座標、z2をZ軸とするXYZ座標というふたつの空間を想定することができます。k(x)の実部はXYz1座標上の点として表すことが出来、虚部はXYz2座標上の点となります。



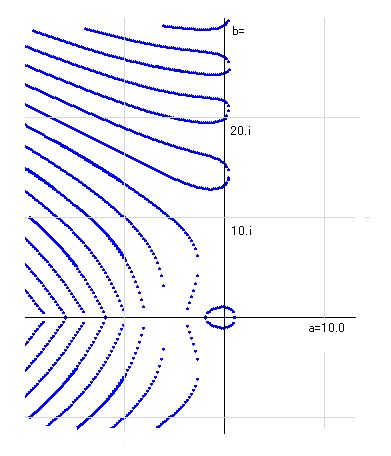
そこでまずはXYz1座標を考え、実部の点を分析します。すると、実部の点が空間上に波のようになっていることがわかります。その波とz=0上のa+biの複素平面との交点が実部の零点となります。その交点が図の上では線として現れるので、それを青線で表現してみます。虚部も同じようにz2=0の複素平面との交点が零ということなので、これを赤線で表現してみます。実部と虚部がともに零のところがリーマンの零点ですから、青線と赤線の交点が答えになります。

右図に於いては、実部が零となるところを青線で示しています。けっこうたくさんの線がありますが、綺麗に並んでいます。







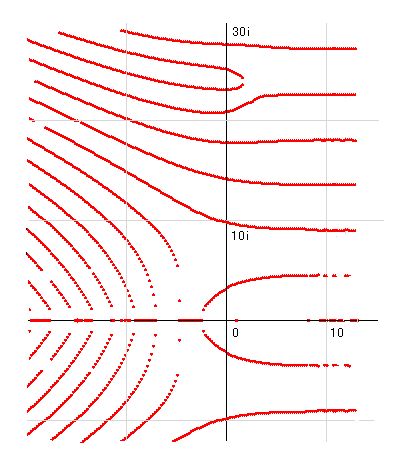
次の図では、虚部が零であるところを赤線で示しています。この赤線もずいぶんたくさんあります。





















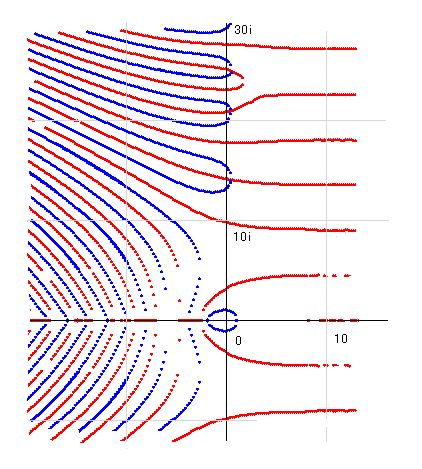
青線と赤線の交点がリーマンの零点です。そこで、ふたつの図を重ねてみました。青と赤がどこで重なるかは図を見ればわかります。ただ、一部、色がかすれたところもあるし、線もたくさんあるので、実際はさらに詳しい図が必要になります。しかし、だいたいのところ、a=0の線の近くとb=0の線上にあることがわかります。a=0の線の近くというのは、さらに詳しく観察するとa=0.5の線上であることがわかります。それ以外のところに零点がないというのがリーマン仮説です。はたしてそのことがこの図からわかるでしょうか。




■


以上の図から直感的にわかることは　　a<0、　1<a　 に零点が存在しないことです。このことはすでに証明されていて、よく知られていることですが、直感でも確認しておくのは無駄ではありません。

左上から下がってくる青線は a=0.5 あたりで繋がって舌のような形になります。これを私は横Ｕ字形と名付けています。この横Ｕ字形が無限大まで続いているということは直感的にわかるのではないでしょうか。そして、どんなに無限大に近い場所でも、横Ｕ字形の内部を赤線が通っていることは確実ではないでしょうか。そして、この赤線は 　1<a　で外に出ているのですから、必ず横Ｕ字形の外に出る時、青線と一度交わることは確実ではないでしょうか。 この交点がリーマン零点なのです。そして、このリーマン零点が発生する場所がだいたい a=0.5 あたりであることは間違いありません。


青の横Ｕ字形が縦に綺麗に並ぶのですから、リーマン零点も縦に並ぶことは間違いありません。それが a=0.5 あたりであることも確実です。ただし、この段階ではまだ a=0.5 上であるとは断言できません。だいたい a=0.5 あたりであるということです。しかし、この「だいたい a=0.5 あたり」ということを確実だと思えるなら、リーマン仮説（リーマン予想）が正しいことも確実となります。なぜなら、証明　ver20 の第２部で証明しているように、「もし、零点がa=0.5上にないなら、a=0.5 から等距離のところにペアで存在しないといけない」からです。

横Ｕ字形はそれぞれある程度の距離をとって並んでいます。ですから、リーマン零点もある程度の距離をとって縦に並びます。横に並ぶことはありえるでしょうか。これについては、直感的と言わなくても「ありえない」と断言できます。絶対にありえません。・・・とは言うものの、数学の証明は絶対あり得ないことでも、そのあり得ないことを証明することを使命としています。ですから、これは大変な作業となるのです。






■　　　　　　＜付記＞



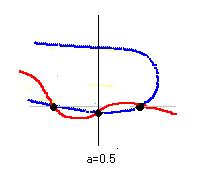
なお、「零点が二つ横に並ぶことはない」ことは直感的にわかりますが、赤線が青線と３つの交点を作って外に出ることはありえます。ひとつは a=0.5 上であり、あとのふたつは a=0.5 から等距離のところであるなら、いまのところ特に矛盾があるとは言えません。

これがあり得ないことを証明しているのがver20証明です。

ver20 証明でリーマン証明は完成したと思っていたのですが、それではまだ不充分ということで、さらに彷徨った結果、ver81 までになってしまいました。まったく・・・疲れましたね。ver81 はいまのところ正しいみたいです。関心のある方は見ていただければ幸いです。