リーマン仮説と非自明の零点の計算方法

revised 2024/09/03

以前アップした説明はあまりにも古いので、書き直すことにしました。最初の頃の説明は参考までに後ろのほうに置いておきます。

非自明の零点（nontrivial zeros）をどうやって計算するかですが、その前に非自明の零点とは何かを説明しておきます。非自明の零点とは、ゼータ関数を複素数化したときに現れる零点のうち、b=0 上でないものを意味します。複素数を　s=a+b*i で表記すると、複素平面は (a,b) というふたつの数で表されます。b=0 上には a=-2, a=-4, a=-6 . . .　と零点が並びます。これを自明の零点（trivial zeros）と言います。trivial　とは言い過ぎではないかと思いますが、日本語では「自明な」と上手に訳出しています。この複素平面上にはもうひとつ零点が並ぶ場所があります。それが a=0.5 上です。ここは虚数にあたる場所で、この線上に登場する零点のことを非自明の零点（nontrivial zeros）と言います。最初の零点は b=14.1327　となり、二番目の零点は b=21.0220　三番目の零点は b=26.0108　と計算できます。この先、どこまでも計算できますが、b=0 上の自明の零点と異なり、零点出現はランダムのように見えます。a=0.5上であることには変わりないので、この現象が無限大まで続くと予想できます。これがリーマン予想です。

しかし、計算した範囲で確認できても、無限大までは計算できないので、絶対にa=0.5上だけであるとは数学的には言えません。絶対確実であると言うためには証明が必要になります。そこで、このリーマン予想を証明しましょうということで、多くの数学者が取り組んできたのですが、１５０年たった今でもまだ証明は完成していません。もっとも、私は証明できたと思っているので、別ページの証明を参照していただきたいのですが、ここではその非自明な零点の計算方法を解説しておきます。

リーマン証明が難しい理由は非自明の零点を計算するのが面倒なことです。コンピュータを使うと計算できますが、計算式が何であるか公表されているものの、その式をどう使うかは数学をかなり勉強した人でなければ理解できません。私の発見した k(s) という式は初心者にも分かりやすい表記になっていて、これをそのまま計算すると解析接続後の値を瞬時に求めることができます。ためしにやってみていただけないでしょうか。実際に計算すれば結果が出るのですから、私の説明が正しいかどうかはすぐにわかります。

その式とは以下のものです。

k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }

この式に登場する zt(s,n) はいわゆるゼータ関数です。もうひとつの ber(s,n) は私の発見した式で、ゼータ関数の発散を抑える働きをします。

zt(s,n) と ber(s,n) の計算は以下の式を使います。

zt(s,n) = 1 + 1/2^s + 1/3^s + . . . + 1/n^s

ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

この式は結構複雑な構造をしていて、zt(s,n)はそのまま計算すると発散してしまいます。ですから、nまでで計算を止めます。ber(s,n) の中に無限式が含まれています。B(r)、つまりベルヌーイ数はｒを増やすと無限大に振動発散してしまいます。また、ｒを無限大まで計算することは物理的に不可能です。便宜上　ｒをどこかで打ち切るのですが、通常はｒとnを同じ値にしておけば問題ない範囲で収束してくれます。ber(s,n) = Σ_[r=0,n] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r という小さな修正を加えます。すると、必要な範囲での有効桁数に収束してくれます。　n=10 , r=10　くらいで問題ありません。もし、有効桁数を増やしたいときは n, r を大きくします。

k(s)を手計算で計算するのは時間がかかりすぎるので、プログラムを作ってあります。関心のある方は「Javaによる多桁計算」ＨＰからダウンロードして使うことができます。

プログラム名は kr(aw,cw,p3) というもので、aw に複素数を入力すると cw に答えがでます。p3が　n,r　にあたるもので計算精度を指定しています。通常は p3=10 くらいにしておきます。また、全体の計算精度も指定する必要があるので、それは ak=100 と指定します。１００桁で計算するということです。このプログラムでは７０００桁まで計算可能になっています。

たとえば、(0.5, 10) の値を計算すると　(1.5448, -0.1153)　となります。(0.5, 15) ならば　(0.1471, 0.7047)　となります。どこに零点があるかを調べるには、その都度計算しなければならないので手間がかかり過ぎます。そこで、これもプログラムを作りました。零点探索プログラムです。b=10 のときの虚部の値はマイナスです。b=15　のときはプラスに変わっています。これはその間に必ず零点があることを意味します。ですから、順次プラスとマイナスに変化する場所を狭めてゆくと、そこが虚部零点となります。実部はマイナスとなる場所が少ないのですが、とにかく出発点となる値を決めて、そこから 0.1 つづ増やした時の値を比べて、符号が変わる場所を探します。そして、符号が変わる場所が見つかったら、その間に零点があるということで、増加させる値を小さくして、再度符号の変わる場所を探します。その作業を繰り返すと、精度のよい零点の値を得ることができます。

このプログラムは「Javaによる多桁計算」HPに入っていますが、解説をしていないので、使えないかもしれません。いずれ、HP全体のリニューアルをするときに、零点探索プログラムの使い方も説明したいと思います。

実部の零点、虚部の零点はたくさんあります。その中から実部も虚部も零である点を探すと、それがリーマン零点となります。最初のリーマン零点が　14.1347...　であることは良く知られています。最初の零点を約５００桁計算しておきました。最初の１は小数点の場所で、次からは数字を示しています。つまり、１４．１３...となります。




■　　　　０から５０までの間にある零点の数

零点がいくつあるかをこの式によって確認してみようと思い立ちました。そこで、グラフを書いて、その零となるところの近傍を調べてみました。

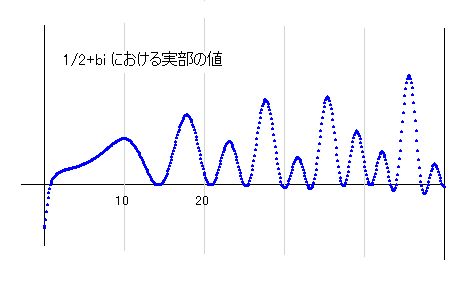
というわけで、その計算結果を載せておきます。実部が零となるところを小さい方から挙げてみます。ピンク色の数字は虚部も零となる、いわゆるリーマン零点です。



0.81954532942
14.1347251421
14.5179196271
20.6540449693
21.0220396387
25,0108575801
25.4915082146
29.7385103001
30.4248761258
32.9350615877
33.6237930728
37.2567417525
37.5861781588
40.7000036428
40.9187190121
43.3270732809
43.9935272863
47.1646901574
48.0051508811
49.7738324776

このグラフから、０から５０の間で実部が零となるのは２０個あることがわかります。




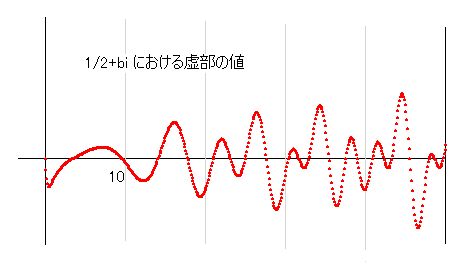
虚部において零となるのは次のとおりです。

3.43621822608
9.66690805613
14.1347251417
17.8455995404
21.0220396387
23.1702827011
25.0108575801
27.6701822176
30.424876123
31.717979949
32.935061593
35.467184292
37.5861781588
38.999209964
40.91871901214
42.3635503920
43.3270732809
45.5930289815
48.00515088116
48.7107766217
49.7738324776

このグラフから、０から５０の間で虚部が零となるのは２１個あることがわかります。
（ak=150, r=512, で計算してあります。）





■　　　　　　k(s) の零線図

k(s)の実部、虚部零点を集めると線となって現れるので、これを零線と名付けます。実部の零点を集めたものが実零線、虚部の零点を集めたものが虚零線となります。その図は以下のようになります。実零線と虚零線の交点がリーマン零点です。








































































■


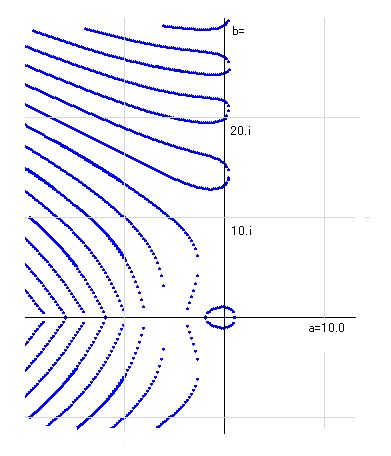
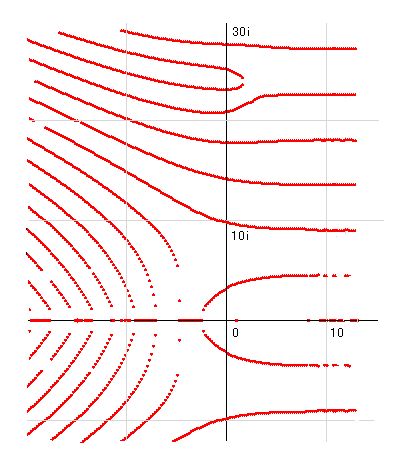
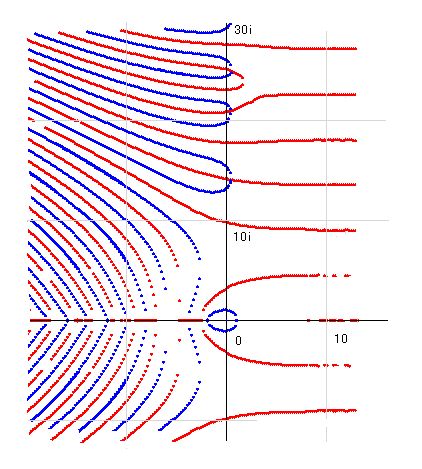
以下の文章はかなり前に書いたもので、素朴なところもありますが、参考までにそのままにしておきます。「hirokuroのリーマン予想証明」の「証明の概略　１の５」にも解説を載せています。



リーマンの零点とは、ゼータ関数を零とする点とのことだと思っている人が多いのですが、先のページで説明したように、私の立場からは、ゼータ関数を成り立たせるk(r)という関数を零とするのがリーマン零点であると考えます。以下、その立場からの説明になりますので、従来の用語法に拘る方々から不満が出るかもしれませんが、その点はご容赦いただきたいと、最初にお断りしておきます。少し我慢して以下の説明を読めば、私の説明も決していい加減なものでないことをご理解いただけると思います。

注　　　掲示板の方のご意見によると、私のk(r)がゼータ関数で、私の定義（理解）が間違っているとのことですが、はたしてそうなのでしょうか。　とすると、以下の説明は書き直さなければなりません。しかし、まだ完全に納得できていないので、そのままにしておきます。読む人が修正しながら理解していただけると幸いです。


さて、ゼータ関数の公式に登場するk(r)ですが、この関数の説明については、従来のマイナス・ゼータの説明の大部分が当てはまります。k(r)を零とするのは、実数の範囲では、-2, -4, -6 . . . などで、複素数の範囲ではリーマンの零点になっています。

私が最初に零点について関心を持ったとき、ためしに、ゼータ関数に 1/2+bi を代入して計算してみました。すると、どうやっても発散、もしくは振動して、収束してくれませんでした。やはりという結果になったので、次にk(r)に代入して、これを算出してみました。おそらくこれで零点は計算できるはずだという思いはありましたが、複素数の扱いに慣れていなかったので、計算が正しく行えるかどうか不安がありました。しかし、幸いにも何とか計算可能な式を導出することが出来、何とかプログラムも作ることが出来ました。そして、それを走らせてみたところ、従来のリーマンのいう零点とまったく同じ値が出てきました。やはり予想通りでしたね。（＾＾）　これで、マイナス・ゼータとは、実はk(r)のことだと確信をもって断言することが出来るようになりました。


■　　　　k(1/2+bi)　の零点を計算する

そこで、ここに零点の計算方法を説明しておくことにします。つまりは、Σ1/n^rの公式にある k(r) を計算するということです。（数学公式３を参照してください。）

Σ1/n^r = k(r)-1/(r-1)/n^(r-1) + 1/2/n^r - r/12/n^(r+1) + 0 + r*(r+1)*(r+2)/6!/n^(r+3) + 0 + ..... という公式がありますから、この r に1/2+biを代入します。


k(r) = Σ1/n^r + 1/(r-1)/n^(r-1) - 1/2/n^r + r/12/n^(r+1) - r*(r+1)*(r+2)/6!/n^(r+3) ..... ということですから、無限計算が二カ所登場します。しかも、k(r)自体が極限値ですから、計算は結構複雑です。そこで、計算の便宜上、この式を３つの部分に分けます。k(r) = Σ1/n^r + 1/(r-1)/n^(r-1) - 1/2/n^r + 1/n^(r-1) * { B(2)*r/(2!*n^2) + B(4)*r*(r+1)*(r+2)/(4!*n^4) + B(6)*r*...*(r+4)/(6!*n^6) + ..... } 　それぞれの式の実部と虚部同士を最後に合計すればk(a+bi)の実部と虚部が計算できます。

そこでまず、Σ1/n^r を計算するプログラムを作ります。Σ1/n^(1/2+bi) = 1 + 1/2^(1/2+bi) + 1/3^(1/2+bi) + 1/4^(1/2+bi) ... となっています。オイラーの公式で、e^(bi) = cos(b) + i*sin(b) となるので、2^(bi) = cos(b*log(2)/log(e)) + i * sin(b*log(2)/log(e))ということになります。また、cos(a)^2+sin(a)^2=1 という公式があるので、分子・分母に cos(b*log(2)/log(e)) - i * sin(b*log(2)/log(e)) をかけると、この部分の分母は１になります。それゆえ、この式の実部は、1+ cos(b*log(2)/log(e))/2^(1/2) + cos(b*log(3)/log(e))/3^(1/2) + cos(b*log(4)/log(e))/4^(1/2) + ... と書くことが出来ます。虚部は、- { sin(b*log(2)/log(e))/2^(1/2) + sin(b*log(3)/log(e))/3^(1/2) + sin(b*log(4)/log(e))/4^(1/2) + ... } となります。

1/(r-1)/n^(r-1) - 1/2/n^r の計算はやや楽です。1/(-1/2+bi)*n^(-1/2+bi) の分子・分母に(-1/2-bi)を掛けて虚数を分子にもってきます。さらにオイラー公式で整理すると、(-1/2-bi) * n^(1/2) * { cos(b*log(n)/log(e)) - i * sin(b*log(n)/log(e)) } / (1/4+b^2) となります。-1/2n^(1/2+bi) は、- { cos(b*log(n)/log(e)) - i * sin(b*log(n)/log(e)) } / 2n^(1/2) となります。両者を合計すると、実部は、 n^(1/2) * { - cos(b*log(n)/log(e))/2 - b * sin(b*log(n)/log(e)) } / (1/4+b^2) - cos(b*log(n)/log(e)) / 2n^(1/2) となります。虚部は、 n^(1/2) * { - b * cos(b*log(n)/log(e)) + sin(b*log(n)/log(e)) / 2 } / (1/4+b^2) + sin(b*log(n)/log(e)) / 2n^(1/2) となります。

1/n^(r-1) * { B(2)*r/(2!*n^2) + B(4)*r*(r+1)*(r+2)/(4!*n^4) + ..... } 　は、1/n^(-1/2+bi)を計算しておいて、あとで{B(2)... } 部分を掛けるというやり方になります。1/n^(-1/2+bi) = { cos(b*log(n)/log(e)) - i * sin(b*log(n)/log(e)) } * n^(1/2) となります。{B(2).. } 部分は、すでにベルヌーイ数は計算してあるので、それを使えるようにします。やっかいなのは、r*(r+1)(r+2) のところです。これを複素数で計算するのは複雑ですから、別途計算するプログラムを作りました。便宜上、rの実部を表すのにra(2)、虚部をrb(2)のように表記します。r(r+1)(r+2)の実部はra(4)、虚部はrb(4)となり、以下同様です。というわけで、{B(2)...} 部分の実部は、B(2) * ra(2) / (2!*n^2) + B(4) * ra(4) / (4!*n^4) + .... と、綺麗に並べることが出来ます。これをbera(n)と表記することにします。虚部も同じ要領で、B(2) * rb(2) / (2!*n^2) + B(4) * rb(4) / (4!*n^4) + .... となり、berb(n)とします。これを先の1/n^(r-1) と掛けるので、全体の実部は、 { cos(b*log(n)/log(e)) * bera(n) + sin(b*log(n)/log(e)) * berb(n) } * n^(1/2) となり、虚部は、 { cos(b*log(n)/log(e)) * berb(n) - sin(b*log(n)/log(e)) * bera(n) } * n^(1/2) となります。

というわけで、３つの部分を合計した値がk(r)になるのですから、実部は、1+ cos(b*log(2)/log(e))/2^(1/2) + cos(b*log(3)/log(e))/3^(1/2) + cos(b*log(4)/log(e))/4^(1/2) + ... + n^(1/2) * { - cos(b*log(n)/log(e)) + b * sin(b*log(n)/log(e)) } / (2 * (1/4+b^2)) + cos(b*log(n)/log(e)) / 2n^(1/2) + { cos(b*log(n)/log(e)) * bera(n) + sin(b*log(n)/log(e)) * berb(n) } * n^(1/2) となります。虚部は、- { sin(b*log(2)/log(e))/2^(1/2) + sin(b*log(3)/log(e))/3^(1/2) + sin(b*log(4)/log(e))/4^(1/2) + ... } + n^(1/2) * { - b * cos(b*log(n)/log(e)) + sin(b*log(n)/log(e)) / 2 } / (2 * (1/4+b^2)) - sin(b*log(n)/log(e)) / 2n^(1/2) + { cos(b*log(n)/log(e)) * berb(n) - sin(b*log(n)/log(e)) * bera(n) } * n^(1/2) となります。

あとはこれを計算するプログラムを書けばよいのですが、式が長いのと無限計算部分があるので、プログラムを書くのはけっこう面倒です。しかし、ベルヌーイ数を使った計算プログラムはすでに何度も作ったことがあるし、無限を扱うプログラムもすでに雛形があるので、たいした問題もなく出来上がりました。（Javaによる多桁計算ソフトを使っています。）



■　　　　計算プログラムを走らせたところ・・・

「プログラムは大した問題もなく出来上がった」と書きましたが、実は、計算結果が予定した数にならず、原因探しにものすごく時間がかかりました。原因はプラスとマイナスを書き間違えていたり、単なる勘違いとウッカリミスなのですが、そういうところがたくさんあるので困ります。ただ、こういうのは毎度のことなので、プログラム作りとはそういうことだと最近では理解しています。ですから、結論としては「たいした問題もなく」と言うことになるのです。

さて、変数がbとnの二つもあります・・・というか、ベルヌーイ数部分も入れて３つもあるのですが、nの極限値計算のところは、手動で動かすようにしてあります。実部が零、虚部も零となるところが零点ですから、とにかく零点を探せばよいということです。そこで、まずは適当にbを定めて計算してみました。たとえば、b=1として、n=16, n=32, n=64 と順番に計算してみました。（手動にしてあるのは、今の段階では厳密な値は必要でないことと、収束するかどうか、目で確かめないといけないからです。ベルヌーイ数部分はあまり計算精度に関係してこないので、１８くらいで打ち切っています。有効桁数は50桁としておきました。）その結果、f(1)=0.143936427077...となり、n=16でも、n=32でも、２０桁程度の一致があるので、精度はこれで充分との結論が出ました。当面、n=32 で計算することにしました。

f(1)=0.1439364... 、f(1/2)=-1.4603545... となったので、1と0.5の間に零点があることは明らかです。そこで、これについては手動では面倒なので、零点を探すプログラムを作り、それにやらせました。すると、b=0.819545329425848... と、けっこう精度の良い結果が得られました。ところが、この数字は、リーマンの零点としては載っていませんでした。おそらく、この虚部が零にならないのだと思われます。そこで、今度は、リーマンの零点といわれているところがこのプログラムで零になるかどうかを確かめてみました。そこで、１４と１５の間の零点を計算したところ、b=14.51920.. という結果を得ました。全然違う数になったので、ひどくがっかりしたのですが、（〜〜）再度計算したところ、b=14.1347251417.. も零になりました。（＾＾）　実部の零点はたくさんあるのですね。HPに挙げられていた数より精度のよい数が得られました。

次の零点も零になるかどうか試してみました。表では21.022040.. となっていたので、その近傍を調べたところ、b=21.0220396387715... という結果になりました。25の近傍も計算してみましたが、b=25.491508... となりました。また、違う結果になり、あせりましたが、先の経験もあるので、ここも再度計算したところ、b=25.01085758...となりました。零点はけっこうたくさんあるのですね。そのつもりで計算しなければなりません。

さて、実部の零点はたくさんあることが判りましたが、リーマンの零点というのは虚部も零と言うことですから、次に虚部を計算することにしました。プログラムとしては同じ構造で、同じようなやり方で計算するのですが、虚部ではなかなか収束してくれず、時間ばかりがかかりました。r=16, r=32, r=64, と増やしていくのですが、この程度の精度では、間違った値に収束します。思い切ってn=1000としてみたのですが、結果が出るのに２分もかかってしまいました。結構時間かかりますね。古いパソコンなので仕方ありません。

このやり方で14.13近傍で零になるところを探してみましたが、14.1347を確定させるのに１時間もかかってしまいました。プログラムの修正か、もしくは別のやり方を検討しないといけませんね。21.022040を確定しようとしたところ、n=1000で１時間掛けて 21.02198まで確定しましたが、誤差が生じています。これはn=2000にすると少し改善します。ですから、零点の計算方法が間違っているわけではありません。



■　　　　零点の分布状況

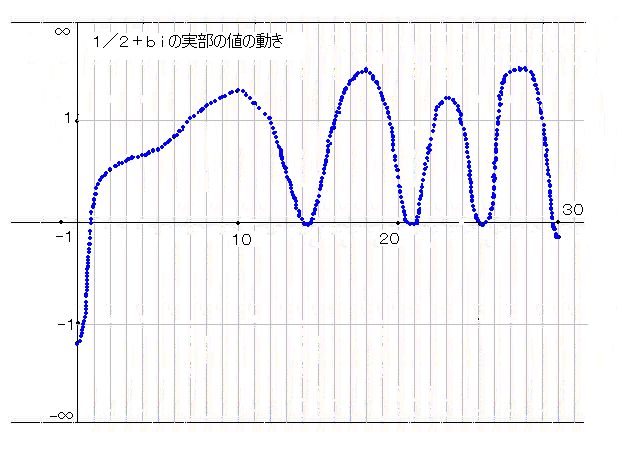
まず、実部f(b)の値がどのように動くかをグラフにしてみました。bが増加に対してf(b)は振動を繰り返します。波形はその都度変化しているみたいですが、どうなのでしょうか。計算上の問題として、ｂを増加させると有効桁も増やさなければなりません。私のPCは古いので、時間のかかる計算には向いていません。まずは、このグラフをご覧下さい。３０までを計算しておきました。グラフを書くプログラムがうまく動いてくれないので、手書きで作ったグラフです。あまり綺麗に書けてませんね。ご容赦下さい。縦軸はATN座標（arctanで縮めてあります。）を使っています。

サイン曲線のように波状に変化しています。特に法則があるようには見えません。bがマイナスの場合も調べましたが、プラスとまったく同じ値が出てきました。計算式を確認したところ、コサイン部分はマイナスもプラスも同じ値になりますし、サイン部分はマイナスが消えるような構造になっているので、f(-b)=f(b) であることは確実です。誤差の段階からf(-b)=f(b)が成り立っているのは面白いことです。





















虚部のグラフは以下のような形になりました。























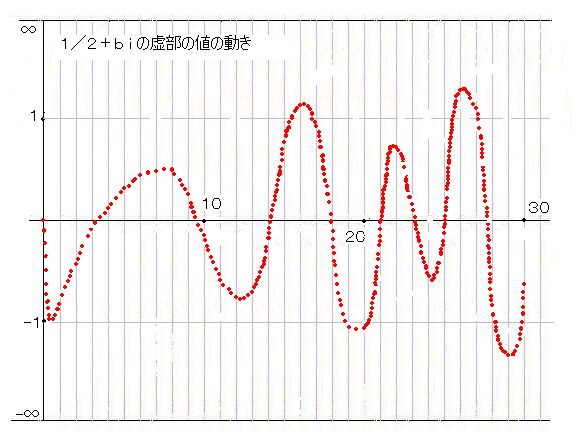
実部と虚部のグラフと重ねてみると、１４．１辺りで、また２１と２５あたりで重なっていることが判ります。そのあたりに零点があることがわかります。そこを集中的に調べれば、詳しい値を得ることが出来ます。