私が最初に発見した数学公式

なにごとも最初にしたことはその人の人生にとって原点となります。私が公式発見に拘るのも、最初の公式発見の楽しさが忘れられないからです。

私が最初に数学公式に関心を持ったのは高校生の頃だったでしょうか。無味乾燥に思えた数の世界にも美しさがあるし、神秘もあるし、実に不思議な世界であることが判ってきた頃です。最初は混乱していると思える状況でも、必ず法則があり、秩序があるのです。たかだか数の世界なのに、現実世界と同様の複雑さがあります。


最初のきっかけは級数の勉強をしていたときのことです。べき乗和というのがあります。今でも、高校生なら誰でも習うはずですが、 f(n)=1+2+3+....+(n-1)+n　という式があります。これが n(n+1)/2 となることは高校の教科書に載っています。

この式の証明は簡単です。f(n)=1+2+3+...+(n-1)+n　と、順序を変えて書き直したもの、つまり　f(n)=n+(n-1)+....+3+2+1　を並べて、加えます。言葉では判りにくいので、書いてみました。
　　
　　　　　　　　　　　　 　　　　
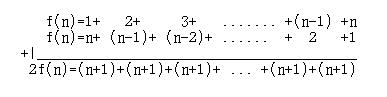
つまりは、右辺に　(n+1)がn個ありますので、n*(n+1)となり、左辺に 2*f(n) がありますので、 f(n)=n(n+1)/2 となるわけです。簡単ですね。

では、次に f(n) = 1+2^2+3^2+4^2+5^2+ ...... +(n-1)^2+n^2 の式はどうなるでしょうか。これも有名で教科書に載っていますが、おそらく多くの人は忘れているのではないでしょうか。　f(n)=n(n+1)(2n+1)/6　です。試しに計算してみると正しいことが判ります。　n=3 とすると、 f(n)=1+2^2+3^2 ですから、 f(n)=1+4+9、f(n)=14です。右辺にn=3を代入してみると、 3*(3+1)(2*3+1)/6=14 と、ぴったり一致します。 n=5 でも、 n=7 でも正しいことはやってみれば判ります。

さて、問題はこれからです。この　f(n)=n(n+1)(2n+1)/6 を証明してみてください。これも教科書に載っています。この程度が出来ないと、高校卒業資格をもらえないかもしれませんが、これが結構難しく、出来る人の方が少ないはずです。というのは、ちょっとした工夫が必要だからです。この工夫を知っていれば簡単ですが、知らないと出来ないのです。高校卒業して何年もたちますと、普通は忘れてしまうものです。ですから出来なくなるのです。出来なかったからと言って心配したり、ひがんだりする必要はありません。

証明方法は、n^3の級数を利用することです。 n^3の級数とは、f(n)=1+2^3+3^3+4^3+....+n^3 のことです。(n+1)^3=n^3+3*n^2+3*n+1 であることは、二項定理などと言わなくても判ると思います。展開してみればよいのです。この式を次のような形に並べてみます。（下図参照）


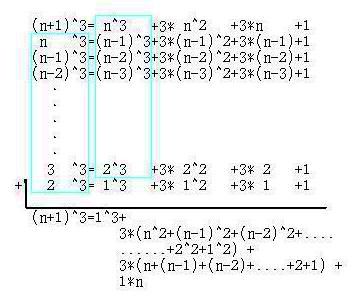
すると、水色の枠内が消えて、n^2の級数が残ります。 f(n) = 1 + 2^2 + 3^2 + 4^2 + .... + n^2 として右辺を整理すると、 (n+1)^3 = 1^3 + 3*f(n) + 3*n(n+1)/2 + n　となります。これを纏めると、3*f(n) + 3*n(n+1)/2 + n + 1 となります。これから、f(n)を左辺に持ってきて整理すると、右辺に(n+1) の共通項が現れるので、それでくくると　(n+1)(n^2+2n-3n/2) となり、さらに整理すると　n(n+1)(2n+1)/2 となります。ですから、最終的には左辺の3を消すために、両辺を3で割ると、
f(n) = n(n+1)(2n+1)/6 が求められます。

長い計算となりましたが、面倒なだけで、難しいわけではありません。


さて、n^2の級数の和が判ったのですから、次にn^3の級数がどうなるかが気になります。これも教科書に載っていますが、同じように、(n+1)^4を使って求めます。計算の過程はn^2 を求めるときと全く同じです。結論は、f(n)=n^2*(n+1)^2/4　です。

同じような関心から n^4 はと考えるのが自然です。これも、参考書に載っています。たしか n^5 もどこかに載っていたと思います。あとは時間は掛かりますが、計算していけばいくらでも求められます。しかし、面倒くさいことこの上ない作業となります。その上、求めたからと言っても何かの為になるとも思えません。ですから、普通は n^5 くらいで終わりにするものです。

しかし、私は何か心に残ったので、その続きを計算してみました。(n+1)^r を展開した後、項目ごとに f(n)　を代入していくわけですから、とても時間の掛かる作業となりました。延々とやり続けまして、n^11 くらいまでやったところで力つきました。さすがに計算に飽きてきました。別に何か判ったわけではありません。大変な計算であることが判っただけでした。


せっかくですから、計算結果を公表しましょう。判りやすくするために、項目ごとの数字を２項定理のような形にしました。
1+2+3+.... =n(n+1)/2 ですが、これは　n^2/2+n/2 と表記して、k(1,0)*n^2+k(1,1)*n とします。つまり、k(1.0)=1/2、　k(1,1)=1/2 となります。
1+2^2+3^2+4^2+.... = n(n+1)(2n+1)/6 ですが、これは　n^3/3+n^2/2+n/6　ですから、　k(2,0)=1/3、　k(2,1)=1/2、　k(2,2)=1/6　となります。
同じように、
k(3,0)=1/4、　k(3,1)=1/2、　k(3,2)=1/4、　k(3,3)=0 　となります。
k(4,0)=1/5、　k(4,1)=1/2、　k(4,2)=1/3、　k(4,3)=0、　k(4,4)=-1/30　となります。
k(5,0)=1/6、　k(5,1)=1/2、　k(5,2)=5/12、　k(5,3)=0、　k(5,4)=-1/12、　k(5,5)=0
k(6,0)=1/7、　k(6,1)=1/2、　k(6,2)=1/2、　k(6,3)=0、　k(6,4)=-1/6、　k(6,5)=0、　k(6,6)=1/42

公表するのも面倒なのでこの辺で止めておきます。とにかくいくつか法則があることは判りますが、だからと言ってどうってことはない感じがしましたので、その当時はそこで止まってしまいました。

それから、一年後くらいでしょうか、当時としては大金をはたいて電卓を手に入れました。せっかくですから、使わないともったいないので、以前止めたところから、電卓で計算をしてみました。たしかに電卓は便利です。入力間違いから、計算ミスをすることは多々ありましたが、計算そのものに疲れることはありません。どんどん結果が出てきます。そのうち、計算そのものに飽きてきまして、結果を眺めていると、以前から気が付いてはいましたが、やはり数字の並び方には法則があることが見えてきました。それを判りやすく表現してみると、

Σ(n^r)=(1/(r+1))*n^(r+1)* { 1+(r+1)/2n+(r+1)r/12n^2-(r+1)r(r-1)(r-2)/720n^4+......　　　}
となります。
例を挙げてみましょう。
r=2 の時は、Σ(n^2)=(1/3)*n^3*{1+3/2n+3*2/12n^2-3*2*1*0/720n^4....} となり、0 の項目を消すと、
Σ(n^2)=(1/3)*n^3*{1+3/2n+3*2/12n^2}　となります。
r=6 の時は、Σ(n^6)=(1/7)*n^7*{1+7/2n+7*6/12n^2-7*6*5*4/720n^4....}　となります。
（注　　　r=1の時は、例外的にこの公式が成り立ちません。というか、奇数の時はある事情で公式は成り立ちません。この問題は、rを非整数まで広げた一般公式の中で解消されました。それについては、後のページで説明します。）

数字が大きくなって書きにくいこともありますが、整理のために su( ) と名付けた数列を導入します。

su(0)=1　
su(1)=1/2　
su(2)=1/12　
su(3)=0　（以下奇数は略）　　
su(4)=-1/720　
su(6)=1/(720*42)　
su(8)=-1/(8!*30)　
su(10)=5/(10!*66)　
su(12)=-691/15!　
su(14)=7/(14!*6)　
su(16)=-3617/(17!*30)　
となります。

r が奇数の時は、r=1 を除いてすべて 0 になります。つまり、
Σ(n^r) = (1/(r+1))*n^r* { 1 + su(1)*(r+1)/n + su(2)*(r+1)!/(r-1)!n^2 + su(4)*(r+1)!/(r-3)!n^4 + su(6)*r!/(r-5)!n^6 + su(8)*r!/(r-7)!n^8 ......　　　} となります。

また、この　su(r) 数列は、便利なことに、下記の法則で計算できることが判りました。つまり、今まで計算していたことのエキスを取り出しただけのことですが、(n+1)^r を使わずに直接　su(r) を計算できるのです。

su(r) = su(r-1)/2! - su(r-2)/3! + su(r-3)/4! - su(r-4)/5! + ...... +- su(1)/r! -+ su(0)/(r+1)!
となります。式の最後にある＋−は符号がその都度入れ替わることを意味しています。

この式を使うと、書き間違いが少なくなり、どんどん計算が進みます。しかも電卓までありますので、r が充分大きいときには、　su(r)=-k*su(r-2)　として、　k=0.025　あたりであることが判ってきました。しかも、k は収束しそうでした。これに力づけられて、さらに計算を進めたところ、ついに k を確定することが出来ました。しかも驚いたことに、既知の数を使って表現できたのです。

k=0.025330..... ですから、 k=1/4pi^2 となっていました。これには大変驚かされました。

そこで、さらに　su(r) の一般解を求めますと、
（注　　　ここでは符号は無視しています。詳しくは公式（３）のページ「Σ1/n の続き」、４）を参照してください。）

su(r)=2/(2*pi)^r { 1+(1/2)^r+(1/3)^r+(1/4)^r+.... 　} 　であることが判りました。

結構、綺麗な式になったと言えないでしょうか。私としては大いに満足しています。