pi、円周率についてはたくさんのHPがありますが、「円周率の計算に関する話題」というHP　（残念ながらHPがなくなってしまいました。）はとても参考になりました。

円周率を求める公式はたくさんありますが、私が使ってみて一番便利だと思ったのはマチンの公式です。こういう凄く便利な公式を発見したマチン (John.Machin, 1685-1751) さんとはどういう人なのでしょうか。あまり数学の本には紹介されていません。
注　　　マチンさんはオランダ人で１７０６年に発見したとのことです。

pi/4=16*arctan(1/5)-4*arctan(1/239)

ところで、この公式は証明されているのでしょうか。公式が正しいことは計算結果から明らかですが、それと証明とは別の話しです。実際上、こういう公式を証明する必要はありませんが、もし万一、証明しようとするなら、どうすればよいのでしょうか。（付記　　　これについては、HBさんからのメールで教えてもらいました。ありがとうございます。高木貞治先生の「解析概論」に載っているとのことですが、何しろ初歩的なことさえ知りませんので、教えていただけると大変助かります。）

円の面積を求めることから円周率が発見されたと思っていたのですが、上記の「円周率・・・」のHPによると、円周を求めることが切っ掛けだったとのことです。そう言われてみると、「円周率」という名前は「円周 (circumference) の長の率」ということですね。名前が起源を表しているわけです。古代に人にとっては、面積より、周の長さの方が大切だったのかもしれませんね。

・・・とは言うものの、私にとっては円の面積を求めることから円周率を実感しましたので、まずは円面積を求めるやり方を解説します。XY座標で、x^2+y^2=1 の図を書いて、その右上部分を積分すれば求められますが、それではあっけないので、もっと素朴に考えます。まずはX軸をn等分して、1/nを一辺とする、円に内接する四角形を描きます。この四角形の面積を合計すると、だいたい円面積に近いものが求められます。あとは、このnを増やしてゆけば、いくらでも円面積に近い値を求めることが出来ます。これを数式化した円面積公式は、pi/4=limΣ{ 1/n√(1-(r/n)^2)} となります。

つまり、n=2として、最初に、1/n{√(1-(1/n)^2)} を計算し、次にn=4として、1/n{√(1-(1/n)^2)+√(1-(2/n)^2+√(1-(3/n)^2)} 、次にn=8として、1/n{√(1-(1/n)^2)+√(1-(2/n)^2)+√(1-(3/n)^2)+.... +√(1-(7/n)^2)} とし、これを無限に繰り返します。すると、pi/4に近づくというわけです。実際にJavaで書いてみたプログラムを載せておきます。enshuritu01.java　（現在修正中です。いずれ再度アップする予定です。）　という名前にしてありますが、動かすときは"Mn.java"に変更してください。計算結果は、3.14に近い数ですが、精度を上げるにはnを大きくしなければなりません。そうすると時間がかかります。

円周を計算する式は、x^2+y^2=1 が円になるので、このXY座標から、pi/2 = limΣ√ (√(1-((r-1)/n)^2) - √(1-(r/n)^2)))^2 + (1/n)^2) という式で計算できます。しかしそれにしてもひどく複雑ですね。電卓やパソコンで計算するのが難しいわけではありませんが、表記が面倒で、あまり綺麗ではありません。

三角関数を使って計算した方が綺麗に書けます。pi/2=lim(n*sin(pi/2n)) です。しかし、この式の中にpiが入っているので、無意味な感じがしてしまいます。

アルキメデスが実際に円周率を計算した方法は、正六角形、正１２角形、正２４角形・・・というふうに、多角形の周囲の長さを求めるやり方だったそうです。正六角形は判りますが、正１２角形、その他はどうやって周囲の長さを求めるのでしょうか？おそらく簡単なのでしょうが、ちょっと考えた程度では判りませんでした。お恥ずかしい・・・。やはりアルキメデスは天才ですね。


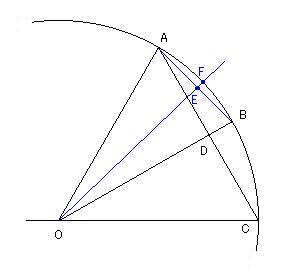
付記　　　おそらく、アルキメデスは以下の方法で円周の長さを計算したのではないでしょうか。円をピザカットのやり方で６等分すると、ちょうど正三角形が６個内接する形になります。

この正三角形のひとつをOACとし、ACの中点Dを通り円周と交わる点をBとします。するとODの長さは√3ですから、DB=1-√3 となります。AD=1/2　ですから、AB^2=AD^2+DB^2　の式からABの長さが判ります。これが内接する１２角形の周囲ですから、同じやり方で２４角形の周囲の長さを求めることが出来ます。つまり、AE=AB/2,　FE=1-OE,　AF^2=AE^2+EF^2　ということです。

これを数式化すると、正六角形の辺の長さをx1とすると、x1=1で、円の直径２に対する比は３です。正１２角形の１辺の長さをx2とすると、x2=√(2-√3)、円に対する比は3.1058...となります。正２４角形の辺 x3=√(2-2*√(1-x2^2/4)) 、正４８角形の辺 x4=√(2-2*√(1-x3^2/4)) と続きます。これを無限に繰り返すと、円周率をいくらでも詳しく求めることが出来ます。ただし、√があるので手計算は簡単ではありません。小数点以下３桁を確定させるのに何時間かかることでしょうか。電卓では数秒で結果が出ますが、手計算だと一日仕事になりますね。大変です。...(´･｀) ﾌｩ･･･

教えてgooにも載っていました。

その他の公式は、数学書にいろいろ載っていますが、良く知られているのが、
pi^2/6=1+1/2^2+1/3^2+1/4^2+1/5^2+......
です。とても綺麗な式ですね。

その他、１８４４年にヨハンターゼの発見した式、
pi/4=arctan(1/2)+arctan(1/5)+arctan(1/8)
などは綺麗です。

オイラーは各種の計算式を見つけていますが、次の式の形は良いですね。
pi^2=12*(1/1-1/2^2+1/3^2-1/4^2+1/5^2-.....
pi/4=arctan(1/2)+arctan(1/3) もオイラーの発見だそうです。凄いですね。
それから、ついでに書いておきますが、自然対数の記号e はオイラーの命名だそうです。このe はオイラーが自分の名前（Euler）の頭文字を使ったものだとのことです。・・・なるほど・・・。

グレゴリー・ライプニッツの公式もあります。
pi/4=1-1/3+1/5-1/7+1/9-1/11+.....
時間はかかりそうですが、ゆっくり収束する公式の代表例でしょうか。

ハットンの公式は、pi/4=3*arctan(1/4)+arctan(5/99) です。

連分数でも計算できます。
pi/4=1/(1+1/(2+3^2/(2+5^2/(2+7^2/(2+9^2/(2+......

その他、非常にたくさんの式がすでに見つかっています。あまりに多いので、探せば自分でもひとつ見つかるかという気がしてきます。

なお、無理数を使うのであまり紹介されていないのが、pi=8*arctan(√2-1) です。これなどみごとにpiになっています。√2とpiが関連していることを示す式として重要です。あと、(-0.5)!=√pi というのも面白いですね。当たり前すぎて書かれていないのが arctan(1)=pi/4 です。 sin(pi/2)=1 などを紹介すると怒られますか・・・。（＾＾）

無理数も含めた式は、円周率を求めるためには意味がありませんが、他の無理数との関係を知る上ではとても興味深いのではないでしょうか。そういう意味の式として私が見つけたのは以下のものです。

log(2*pi)=2*log(ee)+(1-1/12+1/360-1/1260+ ..... )
つまり、ベルヌーイ数で表わすと、log(2*pi) = 2*log(ee)* { 1-B(2)/(1*2) - B(4)/(3*4) - B(6)/(5*6) - B(8)/(7*8) - ..... }
su(n)で表わすと、log(2*pi) = 2*log(ee)* { 1 - su(2) - su(4)*2 - su(6)*4! - su(8)*6! - ...... }
となります。
これは円周率と自然対数の底eeがベルヌーイ数を介して関係していることを示しています。

このような、無理数と無限級数とを併せて使った式なら無限に存在するでしょうから、今度は有限の式で円周率と他の無理数が繋がっている例を探してみることにします。


＜追加　その１＞
「円周率が音楽である」とのHPを見つけました。こういう発想はとても楽しいですね。この方は親切にも実演してくれているので、耳で聞くことが出来ます。思ったよりまともな音楽になっているのには驚きました。アレンジが上手ですね。


＜追加　その２＞　　　　円周率は３か、３．１４か？

数年前の話ですが、学校で円周率を３として教えることになり、それに激しく抗議する意見がマスコミを賑わせたことがありました。おそらく科学者の感覚では３も３．１４も大した違いはないので、３でよいのではないかということなのだろうと思います。科学の実験をしていると感じますが、小数点以下の数字はあまり問題ではありません。どうせ誤差か何かなので、厳密に考えても意味がないのですが。そういう癖が付いてくると、３も３．１４も同じと感じるわけです。ところが、数学者や一般人はそうではありません。それに一度３．１４と習ったというプライドもあります。円周率を３とすることに多くの人が反対したこともまた当然だろうと思います。

ではどうすればよいのか。答は簡単です。実際の生活で円周率を使うことはまずありません。ですから、３でも３．１４でもどちらでもよいのですが、３だと他の数字との区別がつきません。円周率を印象づけるにはやはり３．１４であるほうが文化としては妥当だと思います。ただ、実際の円周率は３．１４１５９２と続くわけで、３．１４であるわけではありません。また、測量とか、実験ではしばしば小数点以下が無視される現実を知っておくことも大切ではないでしょうか。３を円周率として使っても、ほとんど問題ないという現実を知っておくことも大切です。ですから、両方教えるべきなのです。面倒くさいと思う人もいるでしょうが、それを乗り越えるのが教育であり、文化なのです。私などは、３と３．１４を認めるだけではありません。個人的には円周率は３．１４１５９２と覚えています。数学をやった人がこの程度のことを覚えてないのは恥ずかしいですよね。

ですから、こういうのはどうでしょうか。小学生の円周率は３，中学・高校生の円周率は３．１４，大学の数学で使う円周率は３．１４１５９２と教えるのです。そうしておくと、円周率が３．１４という固定概念を壊す効果があります。私はある程度数学にこだわっているので、今後も円周率は３．１４１５９２と主張してゆこうと思います。