hirokuroの公式集

自分の発見したものにはとても愛着を覚えます。新しいものを発見するとか、思いつくなどはすごく楽しいことです。たとえそれが誰にも知られないとか、誰からも評価されないとしても、自己満足することが出来ます。この満足感を味わうと、また味わいたいという気持ちになり、いろいろ努力することになります。

もっとも、学びを続けると、せっかくの自己満足が壊れることもあります。自分では独自のものと思っていたのに、すでに他人が見つけていたことが判ったときなど、その無念さはかなりのものです。しかし、そういうことで意気消沈していては、人生、前には進みません。そういうショックを乗り越えて、今日までやってきました。そして、自分の公式と言えるものがわずかでも残っていることは、充分に満足すべきことだと思います。このうちのいくつかは、これからの学びの中で、周知の公式であることが判明するかもしれません。しかし、それでもかまいません。私は私なりの発見を今後も続けてゆきたいと思います。


n^r の公式

n^r の公式は、私が最初にトライした記念すべきもので、この時の嬉しい記憶が今の私を励ましています。しかし、残念ながら、これはすでにベルヌーイによって見つけられていたとのことで、非常にがっかりしました。

それはそれとして、これは初心者に取っつきやすい公式なので、高校の教科書でも取り上げてもらいたいと願っています。Σn^2 = n*(n+1)/2 とか、Σn^3 = n(n+1)(2n+1)/6 を習うのですから、その先はどうなるか、誰でも疑問を持つはずです。こういう初歩的なところから始めると、難しい感じがしないので、学習意欲が減退しません。

n が4、5、6 ...　の場合も計算すると、Σn^4 = n^2*(n+1)^2/4 、Σn^5=12n(n+1)^2*(2n^2+2n-1)、Σn^6 = 42(n+1)(6n^6+21n^5+21n^4-7n^2+1) となります。この続きについては、すでに別ページで説明しているように、ある法則のもとに式が出来ています。　Σn^r = su(0)n^r/(r+1)+ su(1)(r+)n^(r-1)+ su(2)(r+1)rn^(r-2)+ su(4)(r+1)r(r-1)(r-2)n^(r-4)+ su(6)(r+1)r(r-1)(r-2)(r-3)(r-4)n^(r-6) ..... となっています。su(n) については、別ページで説明しているように、su(0)=1、su(1)=1/2、su(2)=1/12、su(3)=0、su(4)=-1/720...　と続きます。

ただし、この公式は、nが偶数の時に成り立ちます。nが奇数の時もおおむね成り立っているのですが、小さい修正が必要です。そのような修正がいらない厳密な式については、すでに別ページで説明したとおりです。

この公式を見つけるのにすごく苦労しました。ベルヌーイさんがこれをすでに見つけていたらしいのですが、そのように書かれていた解説本の内容は曖昧で、説明も不充分なので、この公式の重要性について、ここで再度強調しておきたいと思います。これは初心者にも判りやすいので、入門の材料として使えると言うことです。


ただ、あえて自己弁護して言うなら、ベルヌーイ数はB(1)=-1/2 である点において、n^r の公式に相応しくありません。su(1)=1/2 であることは、非常に重要です。また、ゼータ関数の公式を見てもわかるように、この公式に登場するのはsu(n)であって、ベルヌーイ数ではありません。つまり、
su(r) = 2/(2*pi)^r* { 1+(1/2)^r+(1/3)^r+'(1/4)^r+.... 　} 　という式をベルヌーイ数で書き直すと以下のようになります。
B(r) = r! * 2/(2*pi)^r* { 1+(1/2)^r+(1/3)^r+'(1/4)^r+.... 　}
これでは、r! が付加されただけで、su(r)の方がより本質的公式であることが判ります。

この公式を、奇数、実数でも成り立つように拡張すると以下のようになります。これはまだ誰も見つけていないみたいです。
su(r) = sin(pi*r/2-pi/2) * 2/(2*pi)^r * { 1+(1/2)^r+(1/3)^r+(1/4)^r+.... 　}

B(1)=-1/2なので、上記の式はベルヌーイ数に相応しくありません。1を代入すると 0*∞ が生じて計算できませんが、極限値として計算すると 1/2 になります。-1/2 ではありません。

これを前提に、奇数や正の実数の範囲にΣn^rを拡張すると、
Σn^r = n^(r+1)/(r+1) * { 1 + su(1)*(r+1)/n + su(2)*(r+1)!/(r-1)!/n^2 +. . . } -r!*su(r+1)
となります。P=n^(r+1)と書いて判りやすくすると、
Σn^r = P/(r+1) + su(1)*P/n + su(2)*P*r/n^2 + su(4)*P*r(r-1)(r-2)/n^4 +.... -r!*su(r+1)
となります。

これはhirokuroの公式として認定しても良いのではないかと思っています。（＾＾）




Σ1/n （自然数の逆数のベキ和、もしくは、調和級数） の公式


調和級数は緩やかに無限大まで拡大する関数です。普通のｘｙ座標だと無限大は図からはみ出てしまいますが、ATN座標だと無限大の姿を目で見ることが出来ます。

右図は、横縦ともにatn(x)で縮めてあります。xが大きいところでは、ほとんど直線的に縦に昇っているので、定規で線を引いてもそれほど間違いではないほどです。

この曲線を数式で表そうと思ってから、見つけるまではずいぶん時間がかかりました。ベルヌーイ数が関係しているので、いくら計算しても収束しないからです。

あることが切っ掛けで、この公式を発見しましたが、誰でも見つけられそうな簡単な構造をしています。証明も、階乗の公式より数段簡単でした。これも入門として使えると思います。高校生レベルでも常識になって貰いたいですね。

Σ1/n = log(n) / log(e)+ 0.577215664... + 1/2n- 1/12n^2+ 1/120n^4- 1/252n^6+ 1/250n^8- 5/660n^10+ ... となっていて

su(r)で表記すると、
Σ1/n = log(n) / log(e)+ 0.577215664... +1/2n- su(2)/n^2- su(4)*3!/n^4- su(6)*5!/n^6- su(8)*7!/n^8...
となります。

これはベルヌーイ数で書いたほうが綺麗です。
Σ1/n = log(n) / log(e)+ 0.577215... -B(1)/n- B(2)/2n^2- B(4)/4n^4- B(6)/6n^6- B(8)/8n^8... となります。

この式はベルヌーイさんが発見したのでなく、私が発見したものですから、その点を譲るつもりはありません。これもhirokuroの公式として認定したいと思います。

（付記 05/09/28）　STUDIO KAMADA さんのＨＰ・２００３年５月の日記に「調和数」とか、「ディガンマ関数」との関係を使って計算できるとの指摘がありました。どういう計算方法か知りませんが、注目されます。ちなみに、オイラー定数は「オイラー・マスケロニの定数」（Euler-Mascheroni constant）とも言うそうです。その他にも興味深い内容が書かれていて、大変教えられました。

「日々の泡」さんの２００４年１２月６日の日記の中でにも興味深い記事がありました。素数の無限積と自然数の逆数の和が等しいことは知られていますが、実際に50000まで計算してグラフにしたところ、なんと両者の差はどんどん拡がってゆき、等しくならないとのことです。ヘェーとはこのことですね。もちろん無限の彼方では等しくなるのですが、こういう現象が本当に起きるのか、自分でも計算して確かめてみなければと思いました。

（付記　05/12/16)　数学大公式集（丸善 p2 ）に調和級数についての説明が載っていましたが、私の式とは異なる形をしていました。あまり綺麗でないので、参考にはなりませんが、関心のある方がいるかもしれないと思って引用しておきます。
Σ(1/k)=C+ ln(n) + 1/2n - Σ{ An/n(n+1)...(n+k-1) }
A(k) は積分記号で定義されていて、ここでは表示できないので、省きます。　A(2)=1/12, A(3)=1/12, A(4)=19/120, A(5)=9/20, となっていました。
なお、Σ1/(2k-1) = 1/2 * (C+ln(n)) + ln(2) + B(2)/8n^2 +(2^3-1)*B(4)/64n^4 + .....　とありました。



階乗 ( n! ) の公式

すでにしつこく説明しているので、繰り返しになって申し訳ありませんが、一応これも私独自のものなので、再度説明させていただきます。　（　05/12/08　　　これは既知の公式だったことが判明しましたので、「私独自」という点は撤回することにします。）

階乗については、スターリングの公式という有名なのがありますが、私の発見した式があれば、スターリングの公式は必要なくなります。

n! = (n/e)^n * √(2*pi*n) * e^(1/12n-1/360n^3+1/1260n^5....)

つまり、
n! = (n/e)^n * √(2*pi*n) * e^｛su(2)/n+su(4)*2/n^3+su(6)*4!/n^5+su(8)*6!/n^7....｝
もしくは、
n! = (n/e)^n * √(2*pi*n) * e^｛B(2)/2n+B(4)/12n^3+B(6)/30n^5+B(8)/56n^7....｝
ということです。

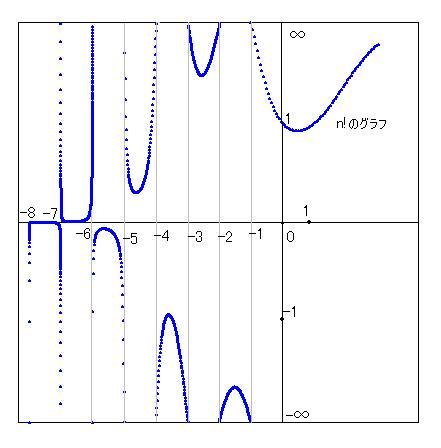
ついでに、n<-1 の時も、上記の式を使って計算が可能となります。計算の仕方は別ページで示したとおりです。参考までにグラフを載せておきます。X軸については、普通の座標を使い、Y軸については、ATN座標を使いました。

n=-1 ,-2, -3 の時は無限になります。(-2.5)! などは有限の値を取ります。大変おもしろい現象だと言えないでしょうか。

(-1.5)!=-3.5449077
(-2.5)!=2.3632718
(-3.5)!=-0.94530872
(-4.5)!=0.27008820

なお、(-r)!=r*pi/r!sin(r*pi) という式が見つかりました。(-r)!がr!から計算できることを示しているので、結構重要な式ではないでしょうか。

その他、Σ1/n^r についても詳しく調べましたが、これがベルヌーイ数で表現できることはすでに知られているようなので、ここでは取り上げません。



(n+1)^(n+1) の公式

(n+1)^(n+1) を展開した式を seki(r) で表現することは、先のページで説明してありますが、これは計算上、そのように推測できると言うだけで、それ以上の研究はまだしていません。seki(r)については、そのページを見ていただくことにして、その研究の過程で見つけた次の式はとても綺麗です。これは記録に値すると思うのですが、どうでしょうか。公式集には載っていないと思うので、ここに載せておきます。

(n+1)^(n+1)=n^(n+1)*e^{1+1/2n-1/6n^2+1/12n^3-1/20n^4....}

(n-1)^(n-1) も同じように綺麗に纏めることが出来ます。

(n-1)^(n-1)=n^(n-1)*e^{-1+1/2n+1/6n^2+1/12n^3+1/20n^4.....}

プラスとマイナスが違うだけで、非常によく似た式になっています。これも知られていないと思われるのでhirokuroの公式と認定しておきます。


その他、それほど凄いというわけではありませんが、以下の式などはとても綺麗だと思うので、載せておきます。

1/n=1/n
1/n(n+1)=1/n-1/(n+1)
1/n(n+1)(n+2)=1/2n-1/(n+1)+1/2(n+2)
1/n(n+1)(n+2)(n+3)=1/6n-1/2(n+1)+1/2(n+2)-1/6(n+3)
1/n(n+1)(n+2)(n+3)(n+4)=1/24n-1/6(n+1)+1/4(n+2)-1/6(n+3)+1/24(n+4)
. . . .
つまり、
1/n(n+1)(n+2)...(n+r) = 1/r! {C(r,0)/n-C(r,1)/(n+1)+C(r,2)/(n+2)-C(r,3)/(n+3)+ ..... C(r,r)/(n+r)}

非常に綺麗に並んでいます。

表紙に戻る　　前のページへ　　次のページへ