■　　　　　　B_th_dif(s) の和分線


B_th_dif(s) の和分線については前ページで述べていますが、B(s)を変形させた関数でも和分線が平らになるだけでなく、a=0 において公式化できる場合が多く、その公式も互いに似ていることから、これらを纏めておきたいと思って、新しいページを作ることにしました。

B(s)とは、ベルヌーイ数を複素数化したもので、B(s) = - s * k(1-s) という関係にあります。ゼータ関数k(s) を計算できるので、B(s)も計算することができます。この関数の極座標角度を表す式が　B_th(s) です。それを縦方向から微分した関数が　B_th_dif(s) となります。和分線とは　B_th_dif(a+b*i) + B_th_dif(1-a+b*i) のことで、a=0.5軸の左右を足したものです。この線が横に流れ、波を打たないことは計算上確認されています。証明は　ver79_ver の中でやってますので、そちらを参照してください。和分線の式が見つかっています。

このページでは a=0 の場合の式が公式化できることを確認します。wa(a+b*i) = B_th_dif(a+b*i) + B_th_dif(1-a+b*i)　と表記することにします。

wa(0+b*i) = ln(b) - ln(2pi) + 13/12b^2 - 119/120b^4 + 253/252b^6 - 239/240b^8 + ...

13/12, -119/120, 253/252, -239/240, 133/132, -32069/32760, 13/12, ...

この数の並びを見ていると、法則があるようで、ないようで、判断に迷います。ベルヌーイ数が　B(2)=1/6, B(4)=-1/3, B(6)=1/42　と続くので、全体的にベルヌーイ数に関係しているだろうと推測できます。また、分子が分母＋1、もしくは、分母ー１　となるのも法則なのでしょう。B(12)=-691/2730 に対応する　32069/32760　が法則にならないので、いろいろ考えていると、ふと　32760-32069=691 であることに気が付きました。これは偶然なのでしょうか。別の数のところでも検証してみるために　b^10 　に注目してみます。ベルヌーイ数は　B(10) = 5/66 なので、133/132 を　66*10 に合わせて整理すると　133*5/660 で、(660+5)/5=133　です。これは気が付きにくいですが、綺麗な法則になっています。

b^14 の係数も計算したところ、13/12 でした。これを　B(14)=7/6　と比較すると、6*14+7=91　で、91/84 = 13/12　となります。法則通りです。

b^16 も計算してみました。4643/8160　でした。これは　B(16)=-3617/510　を変形して、(510*16-3617)/(510*16) = 4543/8160　でぴったり一致します。ベルヌーイ数表の数は約分したものなので、普通は法則の根拠になることはないのですが、今のところ間違いなく法則になっています。

とすると、次の b^18 も計算せずに答えがでます。B(18)=43867/19/42　なので、(19*42*18+43867)/798　となるはずです。その結果は計算精度が足りないので検証できていませんが、「正しそう」というレベルです。

こういう、一見法則がなさそうなところで見つかる法則は嬉しいですね。（＾＾）




■　　　　　　su_th_dif(s) の和分線


su(s) とは　su(s) = B(s)/s! で定義される関数です。この極座標角度を値とするのが　su_th(s) で、それをｂ方向で微分した関数が　su_th_dif(s) です。その和分線ですから、　su_th_dif(a+b*i) + su_th_dif(1-a+b*i) という式になります。

a=0 のときの式を探すと、以下のようになっていました。和分線を　wa(s) で表します。

wa(0+b*i) = - ln(b) - ln(2pi) - 1/12b^2 - 1/120b^4 - 1/252b^6 - ... となります。

ベルヌーイ数で表示すると、

wa(0+b*i) = - ln(b) - ln(2pi) - Σ_[r=2,r=r+2] (-1)^(r/2)*B(r)/r/b^r

次に取り上げる k_th_dif_b(s)　の和分線とよく似た式であることも注目です。





■　　　　　　k_th_dif_b(s)の和分線



k_th_dif_b(s)　という関数があります。これは k(s) の角度である　k_th(s) を縦方向に微分したものです。この関数の a=0.5軸の両側の値を足したものを　wa_b(s) とします。wa_b(s) = dif_b(1-a+b*i) + dif_b(a+b*i)　ということです。

この関数の　a=0 の値を調べたところ、ベルヌーイ数が登場する公式になりました。

wa_b(0+b*i) = - ln(b) + ln(2pi) - 1/12b^2 - 1/120b^4 - 1/252b^6 - ....

これをベルヌーイ数　B(r) で書き直すと、

wa_b(0+b*i) = - ln(b) + ln(2pi) - B(2)/2b^2 + B(4)/4b^4 - B(6)/6b^6 + B(8)/8b^8 - B(10)/10B^10 + ....

となります。つまり、

wa_b(0+b*i) = - ln(b) + ln(2pi) + Σ_[r=2,∞](-1)^(r/2)*B(r)/r/b^r

ということです。 　






■　　　　　　kv_th_dif(s)の公式


kv_th_dif(s) は和分線ではなく、本体の公式です。kv(s) = k(1-s)/k(s) と定義されています。kv_th(0+b*i) の公式は前ページに載せてあります。参考までに再掲しておきます。

kv_th(0+b*i) = b*ln(b) - b*ln(2*pi*e) - pi/4 - 1/12b - 1/360b^3 - 1/1260b^5 - 1/1680b^7 - . . .

これを縦方向に微分すると　kv_th_dif(s) になります。その結果は計算とも一致します。

kv_th_dif(0+b*i) = ln(b) - ln(2pi) + 1/12b^2 + 1/120b^4 + 1/252b^6 + ....

これは　k_th_dif(0+b*i) の和分線とほとんど同じです。マイナスを介して一致しています。このようなことがあり得るのでしょうか。

ちなみに、a=0.5 のとき、kv_th(0.5*b*i) = -2*k_th(0.5*b*i) であることはすでに別ページで解説してあります。

a=0 のとき、k_th_dif(s)　の和分線とは k_th_dif(s) のおおむね２倍となるので、マイナスを介して　kv_th_dif(s) と一致するとは、a=0.5 と同じ現象です。一般の a のときも成り立っているのではという思いが湧いてきました。つまり、k_th_dif(s) の和分線と　kv_th_dif(s) はすべての a においてマイナスを介して一致するということです。

それでは　a=0.1 として検証してみましょう。ln(b) - ln(2pi) + 23/600b^2 + ...　という結果は、符号は逆ですが、一致しています。a=0.2 とすると　1/300b^2 、a=0.3 とすると　-13/600b^2、a=0.4 とすると　-11/300b^2、a=0.5 とすると　-1/24b^2　となって、マイナスを介して一致しています。b^4 以降は計算するまでのまでもないので検証していませんが、間違いなく一致しています。つまり、k_th_dif_b(s) の和分線と、kv_th_dif(s) は同じ構造をしているということになります。なお、k_th_dif_b(s) と _b(s) がついているのは、横方向の微分である　_a(s) と区別するためです。


なお、su_th_dif(s) と　k_th_dif(s) の和分線が似ていることはすでに指摘していますが、kv_th_dif(s) とも似ています。a=0.1, a=0.2 ... と変化させると、ｂについての項目は符号は別として数字は一致します。ですから、su_th_dif(s) も含めて、この３つが同じ構造ということになります。

なお、B_th_dif(s) はやや異なるので、同じという判断は差し控えます。おそらく、何らかの関係はあると思われます。




■　　　　　　k(s)/s! の和分線


以上の公式と数字の動きを見ていると、これらの関数は親戚関係であると言えるように思えてきます。すると、k(s)/s! という関数もまた同じような公式になるのではないかということで、試しにこの関数の　a=0 の式を計算してみました。すると、やや異なるとはいえ、だいたい同じ法則のもとにある公式が見つかりました。

k(s)/s!　の極座標角度をｂ方向で微分した関数の和分線を wa(s) とします。a=0 のときの式は以下のようになります。

wa(0+b*i) = -3*ln(b) + ln(2pi) - 5/4b^2 + 39/40b^4 - 85/84b^6 + 79/80b^8 - ...

ベルヌーイ数は出てきませんが、分子が分母と１の差がある点でB(s)の和分線の式と似ています。ln(b)に３がついているのはかなり大きな違いです。３という数が気になるので、B(s)の和分式を３で割ってみました。すると、最初の　1/12 が　1/4 、次の　1/120 が 1/40 、以下同様に、k(s)/s! の式と同じ数になります。B(s)の分母をa、分子を b として、a-3b とすると、k(s)/s! の和分線の値になります。３で割るのは、約分できるということのようです。

b^4　では　B(4) = - 1/30 なので、(30*4-3)/30*4 = 117/120 で、約分すると　39/40 となります。b^6 では、B(b) = 1/42 なので、(42*6+3)/42*6 = 255/252 で、85/84 となります。 b^8 では、B(8) = - 1/30 なので、(30*8-3)/30*8 = 237/240 で、約分すると　79/80　となります。以下、この法則が続きます。もうひとつやっておくと、B(10) = 5/66 なので　(66*10+5*3)/66*10 となります。結果は　45/44 で計算結果とあっています。

つまり、k(s)/s! も親戚関数だということです。おそらく、和分線も平らで、k(s)/s!を用いてもリーマン証明が可能だろうと思います。





■　　　　　　su_th_dif(s)　と　k_th_dif(s) の和分線が似ていることについて


su_th_dif(s) の和分線と k_th_dif(s) の和分線がほとんど同じであることは驚きですが、別の角度の微分でどうなっているかを調べてみます。おそらく公式化できるとは思えないので、両者の差が何らかの法則になっているのではないかとの予想のもと、微分角度を0にして　-5 から　5　までの横軸の差の値を計算してみました。

微分角度を０にしたところ、su_th_dif(s)の和分線と、k_th_dif(s) の和分線の差はなんと　a　b に関わらず　-3.141592　となりました。ｂを変えても変化ありません。精度を上げても、pi の値のままです。ここまで一致するとは驚きです。

別の角度もトライしてみます。pi/4 としてみましょう。この角度でも　a, b に関わりなく差は一定でした。値は　-4.9205021...　です、。

pi/2 がすでに計算してある　su_th_dif(s) 、k_th_dif(s) の和分線を引けばよいのですが、実際に計算しておきましょう。値は　-3.6757541....　で　-2*ln(2pi) と一致します。

3pi/4 では　-0.3777092....　となります。

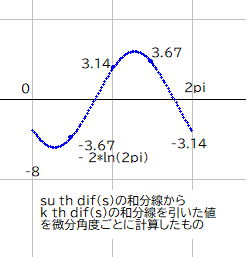そこで、角度を変数th（横軸）として、この値（縦軸）を示すグラフを作りました。右図を見ると、みごとなサイン曲線となっています。このグラフになるようなサイン関数を調べると　y*sin(0+x) = -3.1415, 　 y*sin(pi/2+x) = 2*ln(2pi),　 y*sin(pi+x) = 3.1415, 　y*sin(3pi/2+x) = 2*ln(2pi)　　　この連立方程式を解くと、x=-2.4343988, y=4.8353668　となりました。

a, b に関わらず、初めから誤差なしで成り立つのですから、驚きです。




■　　　　　　k(s)/s の極座標角度を微分した関数の和分線


k_th_dif(s)　と親戚なのはどこまで広がるのかを考えた時、k(s)*s が B(s) と同じになるのなら、k(s)/s はどうだろうかという疑問がわいてきました。そこで、この関数を分析することにします。

k_th_dif(s)/s ではありません。k(s)/s の角度微分です。新しい記号を導入することにして、se(s) = k(s)/s としておきましょう。この関数の極座標角度が　se_th(s) で、それをｂ方向で微分したものが　se_th_dif(s) となります。

和分線は、se_th_dif(a+b*i)+se_th_dif(1-a+b*i) なので、a=0 のときの式を計算によって求めたところ、以下のようになりました。

wa(0+b*i) = - ln(b) + ln(2pi) - 13/12b^2 + 119/120b^4 - 253/252b^6 + ....

B_th_dif(s) の式とマイナスを介してまったく同じです。やはり　se(s) も親戚関数なのですね。





■　　　　　　k(s)*s! としてみると


少し範囲を広げて　k(s)*s! の角度微分和分線を調べてみました。a=0 とすると、

wa(0+b*i) = ln(b) + ln(2pi) + 13/12b^2 - 119/120b^4 + 253/252b^6 - ...

よく似ているので、親戚関数と言えます。s! は大きな数になるはずですが、極座標角度に変換すると、普通の数になるのかもしれません。





■　　　　　　k(s)*(s-1)! としてみると


k(s)*(s-1)! の角度微分和分線を検討してみます。a=0 とすると、

wa(0+b*i) = ln(b) + ln(2pi) + 1/12b^2 + 1/120b^4 + 1/252b^6 + ...

となります。これは　su_th_dif(s) の和分線とマイナスを介して一致します。




■　　　　　　k(s)/s/(s-1)


同じようなやり方で別の関数も分析してみます。k(s)/s/(s-1) などの式はどうなるでしょうか。

角度の縦方向の微分の和分線の式です。

wa(0+b*i) = - ln(b) + ln(2pi) - 25/12b^2 + 239/120b^4 - 505/252b^6 + ...

と、予想の範囲内の式になります。




■　　　　　　k(s)*s*(s+1)


この式の角度微分の和分線は

wa(0+b*i) = - ln(b) + ln(2pi) + 23/12b^2 - 241/120b^4 + 503/252b^6 - ...

となります。




■　　　　　　k(s)*s*(s-1)


ここで問題が発生しました。先の式で　(s+1) 、この式では　(s-1) と変化させたのに、計算結果は同じ式になりました。

wa(0+b*i) = - ln(b) + ln(2pi) + 23/12b^2 - 241/120b^4 + 503/252b^6 - ...

ありえないことですが、どこかにプログラムミスがあるのだろうと思いますが、まだ見つかりません。

どうもおかしいので、(s-3) に替えて計算したところ、また同じ式になりました。プラスやマイナスの数は式に影響を与えないようです。ということは、s!　などの形も意味がないことになります。sの数で和分線の式が決まるということでしょうか。今後のさらなる検討が必要です。