|
ζ(s) ・ゼータ関数 と k(s) の関係 リーマン証明 ver79 の補足として、いくつかのことを説明しておきます。 一番大きな問題は、k(s) という言い方が私独自の表記なので、ゼータ関数との関係がわからない人が多いことです。ver20証明で解説してありますが、そこを読まずに hirokuroリーマン証明ver79 に進むと、k_th(s) が何のことか判らないかもしれません。k(s) とはゼータ関数の別名という面もあり、k_th(s) とは ζ(s) の極座標角度関数を意味します。 なぜ ζ(s) と書かずに k(s) と表記するかというと、一般に通用しているゼータ関数の定義に問題があるからです。ウィキペディアによると、ゼータ関数とは ζ(s) = Σ_[n=1,∞] 1/n^s のことであると説明されますが、これでは実部が1以下のとき収束しません。一般には、ここから先は解析接続というやり方で値を求めますが、そういう複雑なやり方を使わなくても、k(s)を使うと普通の計算で値が求められます。ですから、その限りでは ζ(s) = k(s) なのですが、ζ(s) の収束しないところで k(s) は収束しています。ですから、イクオールで繋ぐことは、私としては抵抗を感じます。実際の k(s) の計算式を見てもイクオールでないことは明らかです。 k(s) = lim_[n→∞] ( zt(s,n) + ber(s,n) ) この式の中の zt(s,n) がゼータ関数に当たります。つまり、zt(s,n) = 1 + 1/2^s + 1/3^s + 1/4^s + .... + 1/n^s ということで、zt(s) = Σ_[n=1,∞] 1/n^s ということです。もし、k(s) = zt(s) とすると ber(s,n) = 0 となってしまい、k(s) の計算式が成り立ちません。ですから 「 k(s)は ζ(s) ではない 」と言わなければなりません。しかし、a=0.5軸の値は ζ(s) では収束しないのですから、リーマン証明で取り上げる関数が k(s) であることは明らかです。つまり、k(s) とはゼータ関数の解析接続後の式であり、これこそゼータ関数の本体であるというか、これこそリーマン証明で取り上げている式そのものだということです。 説明する必要のないほど明らかなことなのですが、いまだに解析接続してリーマン証明を試みている人が多いので、くどいようですが、説明させていただいています。 解析接続は単なる便法であって、k(s) を求めるためのやり方ですが、解析接続を使わなくてもすでに k(s) の計算式が求められているのですから、それを使えばすぐに値が求められます。 k(s) が正しい計算式であることは、最初のリーマン零点の値を正しく求めることができることからも明らかです。その値は 14.134725... ですが、私のパソコンで500桁まで計算してあります。正しいかどうかは一目瞭然です。 最初の零点を約500桁計算しておきました。最初の1は小数点の場所で、次からは数字を示しています。つまり、14.13...となります。 また、a=0.5 のyz座標を k(s) で計算した結果を示しておきます。他の人が計算した図と比較してみてください。b=50までの図です。 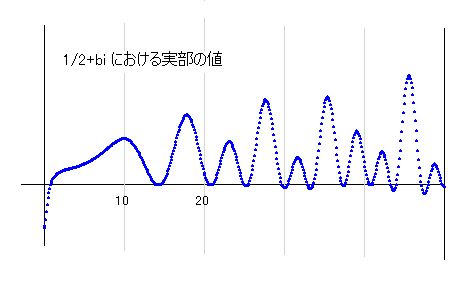 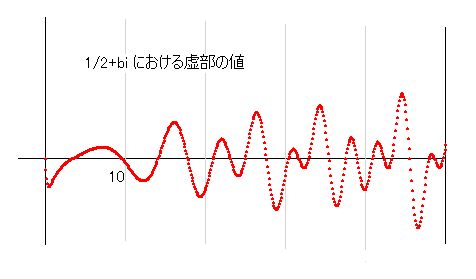 私がもっとも自信をもって示すことができるのは k(s) の零線図です。つまり、ゼータ関数の零線図ということです。これはまだ他の人が計算していないようで、同じ図は見つかりませんが、計算すれば同じ結果になります。 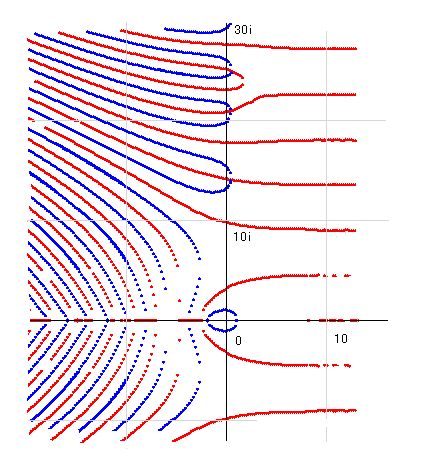 このように、定義の問題を除いて、k(s) はゼータ関数そのものですから、k(s)を用いてリーマン証明にトライすることは何ら問題ないどころか、これ以外のやり方では証明できないということがお分かりいただけると思います。 ■ k_th(s) とは何か ver79証明では、k(s) ではなく k_th(s) が使われます。これは k(s) の極座標角度式です。k(s)=a+b*i とすると、極座標角度θは θ=atan(b/a) となります。ゆえに k_th(s)=atan(b/a) となります。 ver79証明では角度だけを使い、絶対値 k_abs(s) は無視されます。ここで解説が必要なのは、私自身、当初、理解できなかったからなのですが、リーマン零点とは絶対値が零になる点なので、角度は関係ないと思っていました。しかし、絶対値を1として k_th(s) の角度零図を描いてみたところ k(s) の虚零線図とまったく同じ図になりました。これは常識的にありえないことなので、最初は計算間違いかと思いました。計算プログラムのどこかに書き間違いでもあるのだろうと思ったのですが、何度見直しても間違いが見つかりませんでした。結局、正しいということになったのです。 リーマン零点は、極座標で表すと r*(cosθ+i*sinθ) ですから、cosθとsinθの両方が零になることはあり得ません。r が零だからこそ、そこは零点になるわけです。実際、k(s) のリーマン零点では r=0 となっています。ところが、k_th(s) の零線図は r=1 としているのに k(s) 虚零線図と同じになります。最初は不思議な感じがしましたが、数学にはこういうことが起きるのですね。これを事実と受け入れるなら、仮定上の零点のある場所でもこの現象は成り立つわけで、仮定上の零点の場所での k(s) と k_th(s) は同じであることになります。 k(s) のリーマン零点上では θ は零ではありません。絶対値は r=0 となっています。零点ですから当然です。k_th(s) では 虚部の角度 θ=0 で、実部角度 θ=pi/2 、r=1 です。同じ場所で角度が異なることはあり得るかというと、そういう特別なことが起きる点のことを特異点と呼ぶことになっています。実際、リーマン零点と対応する k_th(s) の場所は特異点となっています。零点ではありません。k(s)の仮定上の零点の場所は k_th(s) では特異点なのです。ゆえに、その点を「仮定上の特異点」と呼ぶことにします。零点でないことにご注意ください。 もし、k(s) に仮定上の零点があるなら、k_th(s) には仮定上の特異点があることになります。もし、k_th(s)に仮定上の特遅点がなければ、k(s)にも仮定上の零点がないことになります。 以上の分析を前提に、ver79証明では k_th(s) に仮定上の特異点がないことを証明しているということです。証明を書き上げたばかりなので、証明が確実に正しいかどうかを今言うことはできませんが、今のところ正しそうなので、多くの人に検証してもらいたいと思います。 ご感想、ご質問、その他のご意見は、以下のアドレスまでお寄せください。 表紙に戻る |