sin, cosの複素数公式

sin, cos の公式にs=a+bi　を代入するとそのまま複素数解が得られます。それは誰でも知っているし、簡単すぎます。ここでは、それをスピードアップして、しかも正確に計算できる公式を公表します。精度良く計算してくれるのが良いですね。

どもうすいません。ミスプリントがありました。　÷２　が欠けていますね。 sin_re(s) = ( ee^(-2b) + 1 ) * ee^b * sin(a)　　から　　 sin_re(s) = ( ee^(-2b) + 1 ) * ee^b * sin(a) / 2　へ変更することにします。sin_im(s) も同じ。
単なる書き間違いで、長桁計算の複素サイン関数プログラムは間違っていません。

s=a+bi、　ee=2.718281828 とすると、

sin_re(s) = ( ee^(-2b) + 1 ) * ee^b * sin(a) / 2

sin_im(s) = ( - ee^(-2b) + 1 ) * ee^b * cos(a) / 2

cos(s)は　cos(s) = sin(s+pi/2) で計算できます。

＜補足・追加＞　　　2022/04/04

以前から気が付いていたことではありますが、上記の式を書き直すと次のようになります。このほうが綺麗でしょうか。双曲線関数で置き換えることができます。計算が便利になるというほどのことではありません。

sin_re(s) = cosh(b) * sin(a)
sin_im(s) = sinh(b) * cos(a)

＜追加終わり＞


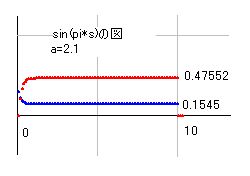
この式の求め方ですが、先にリーマン仮説証明の中でsin(s*pi)を検討したとき、sinの図を掲げました。それが右図です。

この図を見ると、bの大きなところではほとんど平らになっています。この図のままで計算できると良いなと閃いたので、試しに、実部において　a=pi/2 のときにどのような式になるかを計算してみました。すると、綺麗な式になるどころか、近似なしで直接値が求められました。

あとはaの変化により、式がどう変わるかですが、sin(a)を掛けただけの変化でした。あとは、ee^bを掛ければよいので、結果的に上記の式になりました。

虚部については、似たような図なので、式も似ているはずとの推測のもと、同様のやり方で式を求めたところ上記のような結果となりました。

cos(s)は 実部にpi/2を加えてsin(s)を計算したところ、同じ値になりました。 つまり、cos(s) = sin(s+pi/2) ということです。

これで、sin, cos の一般公式より半分ほどの時間で計算できるようになりました。また精度は格段に良くなり、bがかなり大きくても誤差が出なくなりました。

その他のsin, cosの公式

sin,cosの公式はたくさんありますが、ここではその中のごく一部を取り上げます。

f(x)=cos(x)+sin(x)/n という式があったとします。これがサイン曲線になることは判っていますが、どのような式として書き表せるかを調べてみました。プログラムは　hq001.javaです。


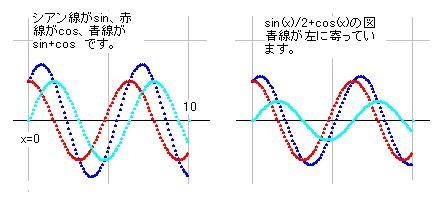
n=1, n=2とすると右図のようになります。

nを増加させるとf(x)はcos曲線に接近します。また高さも減少してcos曲線に近づきます。

そこで、f(x)=a(x)*cos(x-b(x)) とおいて、a(x), b(x) を調べたところ以下のようになりました。

b(x) = 1/x - 1/3x^3 + 1/5x^5 - 1/7x^7 + ...

非常に綺麗な式になりました。これは　x>1 のときの　arctan(x) と同じです。

a(x)はあまり綺麗ではありませんが、有理式として表すことが出来ます。

a(x) = 1 + 1/2n^2 - 1/8n^4 + 1/16n^6 - ....

このとき、a(x)=1+p1/n^2+p2/n^4+p3/n^6+p4/n^8+... となるようにp1,p2,p3...を定義すると、
p1=1/2, p2=-1/8, p3=1/16, p4=-5/128, p5=7/256, p6=-21/1024, p7=33/2048, p8=-3*11*13/2^15, p9=5*11*13/2^17, p10=-11*13*17/2^20, p11=13*17*19/2^22, p12=-11*13*17/2^24, p13=7*13*17*19/2^29/5, ....

検算しておきます。

n=3として、x=7を計算します。cos(7)+sin(7)/3=0.9728977873　f(x)=a(x)*cos(x-b(x))=0.9728977872　となりました。だいたいのところ一致しています。




■　　　　　　cos(x)+sin(x)/x



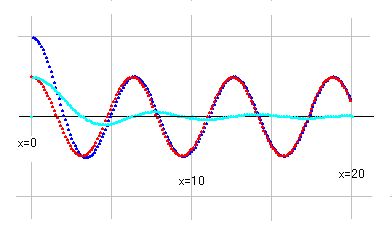
f(x)=cos(x)+sin(x)/x はどうでしょうか。これを図示すると右図のようになります。青線がf(x)で、赤線がcos(x)、シアン線がsin(x)/x です。x>10では、ほとんど青線と赤線が重なっています。

a,b を定数として、f(x)=cos(b*x)+a*sin(b*x)/x としても、図としては大差ありません。







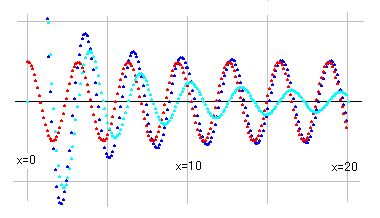
a=5, b=2 としたのが右図になります。b=2なので、波の数が倍になり、a=5なので、シアン線が大きくなり、青線と赤線の重なり方が遅くなります。しかし、xが大きくなると、青線と赤線が完全に重なることは先の図と同じです。







cos(b*x)-a*sin(b*x)/x としても同じで、青線と赤線のズレ方は逆ですが、a*sin(b*x)/x は零に近づくので青線と赤線はいずれは完全に重なります。