派生した公式(その2)
■ kv(s)の分析
(revised 10/10/31)
kv(s) = k(1-s)/k(s) と定義されます。このkv(s)はリーマン証明で非常に重要な役割を果たした式で、リーマン零点の発生に関係しています。とても面白いところがあるので、分析する価値があるように思います。
k(1-x)/k(x) = x! *2*cos(pi*x/2) / { x*(2*pi)^x } であることも確認済みです。
今回公表するのは、s=a+b*i で、a=0.5のときのkv(s)の極座標表示の角度を計算する近似公式です。kv(0.5+b*i)の絶対値は1なので、角度が判れば実部、虚部を計算できます。近似式なので b がある程度の大きさであることが要求されますが、b→∞ の姿を捉えるには近似式で充分です。
さらに高度な近似式を計算することは、時間をかけさえすれば可能ですが、今のところ、式全体を記述する法則は見つかりません。これが見つかると近似式ではなくなるのですが、いずれもっと工夫して探してみるつもりです。(その後、完全イークオル公式が見つかりました。このページの最後を参照してください。10/09/29)
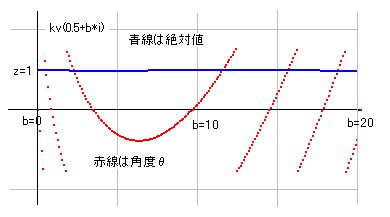
まずは、kv(s)の極座標を考えます。青線はベクトルの絶対値で、赤線は角度を示します。絶対値は複素数の長さでもあります。この青線は a=0.5 の場合、常に1なので、計算する必要はありません。角度は最初だけ右肩下がりですが、b=7 あたりから右肩上がりになり、bが大きくなるに従い、しだいに傾きは大きくなります。
角度を示す式を kv_θ(s)と表記することにします。すると、
kv_θ(0.5+b*i) = b*ln(b) - b*ln(2*pi*e) - pi/4 + 1/24/b - . . .
となります。
まずは、この式が正しいことを計算により示しておきます。b=100のとき、kv(a+bi)の値は、kv_re(s)=9.9988536E-1 kv_im(s)=1.5141283E-2 です。絶対値は 0.9999999... となります。角度は、a=kv_im(s)/kv_re(s) θ=atan(a) なので、θ=1.5141862E-2 となります。
さて、近似公式で計算するとどうなるでしょうか。b=100として、上式に代入します。すると、kv_θ(0.5+100*i)=175.9443305 を得ます。角度は2*πごとにくるくる回っているので、θとθ+2*pi は同じです。ゆえに、175.9443305 から 56*pi を引くと 1.5141899E-2 となります。これはkv(s)から計算した値とほとんど同じです。
bを大きくすると、誤差はさらに減少します。b=500のとき、kv_re(s)=-8.5515518E-1、kv_im(s)=-5.1837208E-1 となり、絶対値は 1.0、角度θ=5.4494619E-1 です。これを上式で計算すると、θ = 1687.580201 - pi*537 = 0.544946 となります。
さて、近似公式をどのように求めるかを説明しておきます。
kv(s) = s!*2*cos(pi*s/2) / s / (2pi)^s という公式があります。これがこの分析の前提です。a=0.5のときの近似式なので、(0.5+bi)!*2*cos(pi*(0.5+bi)/2) / (0.5+bi) / (2pi)^(0.5+bi) と書き直します。この式のひとつひとつを順次分析します。
まず、(0.5+bi)! ですが、これを実数階乗の公式に代入します。実数階乗公式はbがプラスなら複素数でも問題なく成り立ちます。s! = (s/e)^s * √(2pi*s) * e^(f(s)) なので、この式も分割して、それぞれ分析します。
■ (0.5+b*i)^(0.5+b*i)
(s/e)^s は s^s から成り立つので、s=0.5+b*i を代入して、(0.5+b*i)^(0.5+b*i)を分析します。これは s^0.5 * ( cos(b*ln(s)) + i*sin(b*ln(s)) ) なので、s^0.5 と cos(b*ln(s)) + i*sin(b*ln(s)) を別々に分析します。
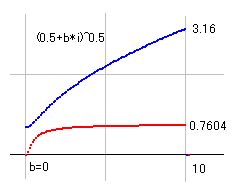
(0.5+b*i)^0.5 を極座標として図示したのが右図です。青線が絶対値、赤線が角度(ラジアン角)を示しています。この式の公式化は、あとの式との関連があるので、後回しにします。
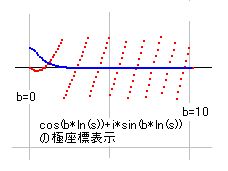
そこで、cos(b*ln(s)) + i*sin(b*ln(s)) を分析します。右図はその極座標図です。角度はpiの枠に入るようになっていますが、実際の複素数ベクトルは bの増加と共にくるくると回転し、角度増加は連続していることにご注意ください。式の計算結果はpiの中に収まるように調節されて出てくるので、増加の計算結果を得ることが面倒です。そこで、まずは、この角度増加の傾きを計算し、それを積分することで角度公式を求めることにします。
f_θ'(s) = ln(b) + 1 - 1/8b^2 +3/64b^4 -5/384b^6 + 7/2048b^8 . . .
これを積分すると f_θ(s) = b*ln(b) + 1/8b -1/64b^3 + 1/384b^5 - 1/2048b^7 . . . となります。
ここでひとつの法則が見つかりました。8=2^2*2, 64=2^4*4, 384=2^6*6, 2048=2^8*8, となっています。この続きがどうなるかは明らかです。また、これをプログラム化して計算した結果、誤差なしに正しい答えが出てきました。
■ 2*cos(pi*s/2)
2*cos(pi*(0.5+b*i)/2) の極座標図は単純なので、割愛します。角度公式はとても綺麗な形になっています。
e^(b*pi)=P と表記することにします。すると f03_θ(s) = -pi/4 + 1/P - 1/3P^3 +1/5P^5 - 1/7P^7 + . . . となります。
■ (2pi*e)^s
(2pi)^sとe^sはひとまとめにして(2pi*e)^sとして考えます。(2pi*e)^(0.5+b*i) の極座標の角度公式は以下のように完全イクオールになります。
f_θ(s) ≡ b*ln(2pi*e)
ln(2pi*e)=2.837877067 です。定数掛けるbなので、直線増加となります。
■ e^f(s)
f(s)はベルヌーイ数が含まれるので、このままでは計算できません。実数階乗公式の場合は、sに適当な大きさの正の整数を加えて計算し、そこから順次割ってゆくことにより誤差無しの解を得ます。f(s)にはそのようなやり方が通用しないので、階乗の公式から逆に計算することにします。
e^f(s) = s! / (s/e)^s / √(2*pi*s) これが計算式です。ln(e^f(s)) = f(s) です。
角度公式はある程度の精度で見つかっていますが、全体を表示する法則が見つからないので、さらなる検討が必要です。それで、やや面倒ですが、e^f(s)に関係するすべての式を挙げておくことにより、今後の研究の土台としたいと考えています。f(s) と e^f(s) の実部式( _re)、虚部式( _im)、絶対値式( _abs)、角度式( _θ)の4つがあるので、合計8つの式を挙げておきます。すべて a=0.5の場合です。
e^f_re(s) = 1 + 11/288b^2 -
e^f_im(s) = -1/12b + 0.0146798.../b^3
e^f_abs(s) = 1 + 1/23b^2 - 13/5760b^4 + ...
e^f_θ(s) = -1/12b + 13/720b^3 - 37/20160b^5 + 3/1792b^7 . . .
f_re(s) = 1/24b^2 - 1/160b^4 + 1/896b^6 - . . .
f_im(s) = -1/12b + 13/730b^3 - 37/20160b^5 + 3/1792b^7 . . .
f_abs(s) = 1/12b - 11/1440b^3
f_θ(s) = -pi/2 + 1/2b - 1/120b^3 + 47/6250b^5
このうち、kv(s)の角度公式に使うのは e^f(s)_θ だけですが、f(s)_im とまったく同じであるのは面白いことです。
また、f(s)_reの式には法則があることが判ります。24=2^3*3, 160=2^5*5, 896=2^7*7 です。次がどうなるかは明らかで 2^9*9=4608 となります。実際に計算してみると、これで正しいことが判ります。その次は 2^11*11=22528 となります。cos(b*ln(s)) + i*sin(b*ln(s))の角度公式とよく似ているのは偶然でしょうか。あまりにもうまく出来すぎています。
■ s^0.5 * √(2pi*s) / s
この三つの式は、角度については合計すると零となります。
s^0.5 とは √(s)のことです。√(2pi)は実数なので、角度に影響を与えません。それゆえ、√(2pi*s)の角度は√(s)と同じです。先に√(s)があるので、これを掛け合わせる、つまり角度については足し合わせるとsと同じになります。分母のsと同じなので、割り算は角度については引き算になるので、同じ値を引くので零となります。
■ 結論
以上の角度公式を合計すると、
kv_θ(0.5+b*i) = b*ln(b) - b*ln(2*pi*e) - pi/4 + 1/24/b + 7/2880b^3 + 20123/20160b^5 + . . .
となります。
この式のメリットは、bが大きいとき kv(s)では計算時間がかかりますが、kv_θ(s)だとすぐに結果が出ることです。a=0.5の場合、絶対値は常に1なので、角度から実部、虚部の値が計算できます。
試しに b=45.0のときを角度公式から計算してみます。θ=42.810872 となります。pi*14を引くと -1.171425 となります。abs=1.0 なので、tan(θ)=-2.369374 b=2.369374*a となるので、a^2+b^2=1 に代入すると、a=+-0.3888389 を得ます。ゆえに、b=+-0.9214057 で、tan(θ)がマイナスなので、aとbの符号は逆でなければならず、a=0.3888389 なら b=-0.9214057、a=-0.3888389 なら b=0.9214057 となります。どちらの組み合わせかは、このままでは判らないので、別途研究したところ、2*πごとのリズムになっていたので、t = ceil( kv_θ(s)/2pi ) として、x = kv_θ(s)-t*2pi とします。この x が pa=1.5707963 より小さいときは 実部がプラス、2pi-pa=4.7123889 より大きいときはプラス、それ以外はマイナスと判定されます。虚部については、x がpiより小さいときはプラス、大きいときはマイナスと判定されます。ですから、上記の例では、θ = 42.810872-pi*12 = 5.111760157 となるので、実部はプラス、虚部はマイナスということですから、a=0.3888389, b=-0.9214057 のほうを選ぶことになります。
これをkv(s)で計算すると、a=0.38883893 b=-0.9214057 となっています。
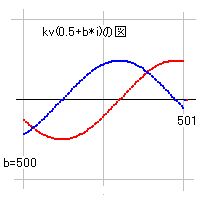
さて、ここでこの近似公式がいかに便利かを示しておきます。bが大きいとき、kv(s)の計算には精度が必要になるので、時間がかかります。たとえば、b=500から0.01の幅で100個計算すると501まで計算したことになります。これをkv(s)で計算すると ak=800, p3=25 で589秒もかかりました。その図が右のものです。
これを近似公式で計算すると、ak=100でわずか2秒で終わりました。その結果は先の図とまったく同じなので掲載しませんが、bが大きくなればなるほど誤差は減少します。
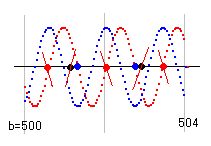
さて、次の章を先に読んでいただきたいのですが、その内容の再確認をここでしたいと思います。kv(s)の図で、虚部曲線が増加中に零になる点(赤点)をk(s)の虚部局線下りが通ります。また、実部曲線と連動してk(s)の実部曲線も動いていて、kv(s)の虚部曲線下り線が零となる点(青点)を実部線が通ります。この点の左右どちらかの近傍にリーマン零点(黒点)が必ず存在し、そこをk(s)の実部・虚部の両方の曲線が通るのですが、虚部曲線は必ず上り線です。実部曲線は上りだったり、下りだったりします。
これで、リーマン零点の発現場所と個数がはっきりします。
■ kv(s)とk(s)の関係
kv(s)とk(s)の関係については、すでに知っているということで説明してきましたが、hirokuroのリーマン証明を読んでない人は何のことかわからないでしょうから、ここで再度説明しておきます。
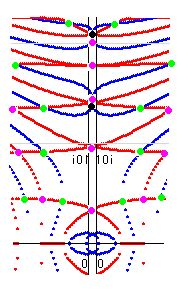
kv(s)=k(1-s)/k(s) これがkv(s)の定義です。k(1-s)とk(s)はa=0.5を中心に、実零点、虚零点については左右完全対称です。右図はk(1-s)とk(s)の零点を重ねたもので、青(実部線)と赤(虚部線)の交点を緑点、同じ色の線の交点をピンク点、リーマン零点では両方の実虚線が交差するので、合計4本の線が集まっています。これを黒点で表示してあります。
さて、リーマン零点上では、0/0が実行されていますが、k(1-s)/k(s)が零にならないことはすでに証明されています。kv(s)に実虚零点はないからです。ここで注目するのは緑点とピンク点です。緑点とは(0+b*i)/(a+0*i) もしくは (a+0*i)/(0+b*i) が実行される場所のことです。これがどうなるかは計算してみれば判ります。つまり、前者がb/a*i 後者が -a/b*iで、どちらも実部は必ず零となり、kv(s)の実零線が通る場所となります。
ピンク点は (0+b1*i)/(0+b2*i) もしくは (a1+0*i)/(a2+0*i) となる場所のことで、前者がb1/b2、後者がa1/a2 となり、どちらも実数ですから、虚部が零となります。つまり、ここはkv(s)の虚零線が通る場所となります。事実、kv(s)の零線図を描いてみると、みごと緑点、ピンク点を通っています。図は結構複雑なので割愛しますが、以上の説明で、それも当然のこととおわかりいただけると思います。
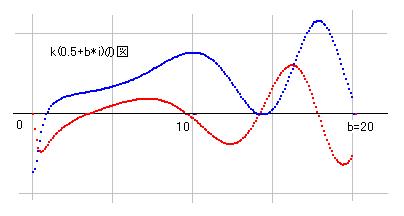
さて、kv(s)の全体は図示しにくいのですが、a=0.5の範囲ではそれを図示することも可能になります。右図はa=0.5のときのk(s)の図で、b=14.1347 にリーマン零点があることが判ります。
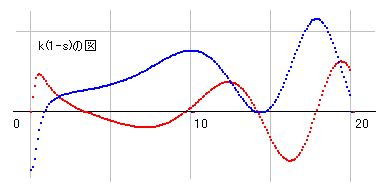
右図はa=0.5のときのk(1-s)の図ですが、k(s)と実部は全く同じ、虚部はマイナスを介して同じ値を取っています。ですから、虚部零点の場所は同じです。
さて、a=0.5において k(1-s)/k(s)を実行するとは、任意のaの場合と同じなので、kv01図とkv09図を重ねたときに生じる異なる色線の零点はリーマン零点なので黒点、同じ色の零点はピンク点となります。黒点はkv(s)の零点にならないので、kv(s)の零線は通りません。しかし、ピンク点はkv(s)の虚零線が通ります。
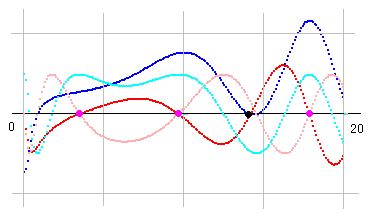
右図はk(s)図とkv(s)図を重ねたものですが、予想通りの図になっています。第一ピンク点は例外ですが、その後のピンク点の間にk(s)の実部零点がふたつあり、そのうちのひとつを虚零線(赤線)が通過してリーマン零点を作り、もうひとつをkv(s)の虚零線(ピンク線)がとおります。
kv(0.5+b*i)の角度公式の意味は、bが大きいときのピンク線を描くことを簡単にさせるということであり、角度が常に増加すると言うことは、ピンク線は必ず波となり零を繰り返し通過すると言うことであり、そこにピンク点が発生します。ピンク線の零点がすべてピンク点になるのではないので、再度、説明しますが、b=1あたりに最初の零点があり、次の零点が例外のピンク点です。3番目は普通のピンク点であり、4番目の零点は実零線(青線)との交点ですが、特に名前はついていません。5番目の零点がピンク点であり、k(s)の虚零線(赤線)が通過しています。このように奇数番目の零点がピンク点となっています。
偶数番目の虚零点(非ピンク点)の近傍にリーマン零点が必ず存在します。その場合、虚零点を越える場所か、越えない場所かはその都度変動し、特に法則があるようには思えません。
さて、k(0.5+b*i)とkv(0.5+b*i)の間にはサイクルの一致が見られることが判りましたが、当初、極座標角度が両者で一致することを意味しているだろうと理解しました。しかし、実態はやや異なり、プラスマイナスが反対で、kv_θ(s)のほうが2倍の早さになっていました。2倍の早さとは傾きが2倍と言うことです。やや驚きですが、これでサイクルが一致するのでしょうか?計算間違いかとも思ったのですが、どうもk(s)のほうがpiごとに繰り返しが起こるのに対し、kv(s)では2piごとに起こっていることが原因のようです。とにかく、繰り返し(サイクル)という点では k(s)とkv(s)は一致するということになります。
角度については、b>0で kv_θ(s)≡2*k_θ(s) なので、kv_θ(s)の式を使って k_θ(s)を計算することが可能になります。
■ kv(0.5+b*i)の完全公式
(update 10/10/01)
すでにkv(0.5+b*i)の近似公式は公表していますが、今回、完全公式も見つかったのでご紹介します。非常に綺麗な形をしているので、久しぶりに大満足です。
ここで言う完全公式とは e^f(s)の極座標角度についての完全公式です。これが判るとkv(0.5+b*i)の全体も自動的に明らかになります。そこで、まずは e^f_θ(s)を説明します。e^f_θ(s) = f_im(s) なので、f(s)の虚部式とも一致しますが、当面は角度に焦点を当てています。
すでに公表した角度の近似公式は以下のものです。
e^f_θ(s) = -1/12b + 13/720b^3 - 37/20160b^5 + 3/1792b^7 . . .
この続きがどうなるかは計算精度の限界を超えるので、簡単には判りません。しかし、e^f(a+b*i)の計算結果が有理数になるので、何か法則があるのではないかと調べたところ、ある程度確定する有理数が出てきて、そこに法則があることが判りました。
a=0.5 のときが -1/12b + 13/720b^3 - 37/20160b^5 + . . . となるので、aが別の値の時どうなるのかを調べると、
a=1 のとき -1/12b + 29/360b^3 - 17/252b^5 + . . . となり、
a=2 のとき -1/12b + 119/360b^3 - 1597/1260b^5 + . . . となり、
a=0 のときは確定しやすくて 1/12b - 1/360b^3 - 1/1260b^5 - 1/1680b^7 - . . . となります。
最初の項目は 1/12 となると判断できます。次の項目は 1/360, 29/360, 119/360 ですから、分母は360になると言えますが、a=0.5のときが360*2=720になっているので、720と考えます。次の分母は 252*5=1260 で、1260*16=20160 なので、分母は20160となると考えます。
a=3 以上はなかなか確定しにくくなるので、分母が確定するとして a=0.1からa=0.9までを計算します。すると、有理数がよりはやく見つかります。その結果、最初の項目が 1/12であることはすぐに判りますが、次の項目は (30*a^2 - 1) / 360 という結果になります。次の項目は (105*a^4 - 21*a^2 + 1) / 1260 となります。その次はなかなか確定しないので、ここで推測を入れます。
分母が 12, 720, 20160, 1680 などが出てきますが、これを階乗と関係付けるなら、2/24, 1/720, 2/40320, 2160/10! と並びます。ちょうど、4!, 6!, 8!, 10! と並んだので、これを基準として整理すると、最初の項目は 2/24、次の項目は 2a^2/24 - 2/720、その次は 2a^4/24 - 12a^2/720 + 32/8! となります。こうなるべきだとして計算すると、その次の式が 2a^6/4! - 30a^4/6! + 480a^2/8! - 2160/10! となる可能性があるという程度のことが見えてきます。
しかし、これ以上はどうしようもないので、極限値計算の精度を上げて、より早く収束値が見つかるような工夫をしました。その上で、a=0の続きを計算したところ、403200/12! 167166720/14! という結果が出ました。167166720 = 2^8*3^3*5*7*691/14! です。ここに 691 という数があることに気が付きました。この数はベルヌーイ数 B(12)=-691/2730に登場する 691 と同じです。偶然のようには思いましたが、試しに B(r)で整理してみたところ、1/360=B(4)/3/4, 1/1260=B(6)/5/6, 1/1680=B(8)/7/8, 1/1188=B(10)/9/10, 167166720/14!=B(12)/11/12 となりました。符号まで一致しています。これだけ綺麗に並べば、法則と認定しなければなりません。f(x)がB(r)で記述できるように、f(s)の角度もB(r)で表現できるのです。
そこで、B(r)を基準に整理してみます。すると、
B(2)*b^2/2 + B(4)/3/4
B(2)*b^4/2 + B(4)*b^2/2 + B(6)/5/6
B(2)*b^6/2 + B(4)*b^4*5/4 + B(6)*b^2/2 + B(8)/7/8
B(2)*b^8/2 + B(4)*b^6*7/3 + B(6)*b^4*7/3 + B(8)*b^2/2 + B(10)/9/10
この並び方を見ると、次がどうなるかはだいたいのところ判ります。しかし、一部新しい数が出てきているので、そこがどのような法則になっているかを調べなければなりません。
3番目の並びに 5/4 が出てきます。次が 7/3 です。次がどうなるかは判りません。これは計算してみました。
次の列は 1/2, 15/4, 7, 15/4, 1/2, 1/11/12 と並んでいました。
その次の列は 1/2, 55/10, 165/10, 165/10, 55/10, 5/10, 1/13/14 と並んでいます。
これ以上はなかなか収束してくれないので、かなり苦労しましたが、どうも 1/2, 91/12, 1001/30, 429/8, 1001/30, 91/12, 1/2, 1/15/16 となるようです。1001=7*11*13, 429=3*11*13 です。前の列では11が目立ちますが、この列では13が目立ちます。おそらくこれが法則のなのだろうと推測して、5, 7, 9, 11, 13 と並べてみました。つまり、最初の列が 3/6, 3/6 次の列が 5/10, 5/4, 5/10 次が 7/14, 7/3, 7/3, 7/14 次が 9/18, 9*5/12, 9*7/9, 9*5/12, 9/18 次が 11/22, 11*5/10, 11*5*3/10, 11*5*3/10, 5*11/10, 11/22 次が 13/26, 13*7/12, 13*7*11/30, 13*3*11/8, 13*7*11/30, 13*7/12, 13/26
この中に何か法則はないかと見ていたところ、一番目がすべて1/2であることは良いとして、2番目が12を基本としているように見えてきました。そこで、並べてみると、1/2, 5/4, 7/3, 9*5/12,11/2, 13*7/12 ということです。これを通分すると、6/12, 15/12, 28/12, 9*5/12, 6*11/12, 13*7/12 となります。すると、分子がr*(2r-1)の形になっています。これでひとつ法則を発見しました。
こういう具合にひとつひとつ法則を見つけてゆく過程で、全体的には次のような法則があることが判りました。
最後の列は 14!/14!/2!=1/2, 14!/12!/4!=91/12, 14!/10!/6!=1001/30, 14!/8!/8!=429/8, . . . と続きます。あとは全部同じ法則です。その前の列は 12!/10!/4!=11/2, 12!/8!/6!=33/2, その前の列は 10!/8!/4!=9*5/12, 10!/6!/6!=7 あとは明らかなので、省略します。
この法則と先のB(r)の法則とを合体させると、
B(12)/12/11 + B(10)*10!*a^2/10!/2! + B(8)*10!*a^4/8!/4! + B(6)*10!*a^6/6!/6! + B(4)*10!*a^8/4!/8! + B(2)*10!*a^10/2!/10!
B(14)/14/13 + B(12)*12!*a^2/12!/2! + B(10)*12!*a^4/10!/4! + B(8)*12!*a^6/8!/6! + B(6)*12!*a^8/6!/8! + B(4)*12!*a^10/4!/10! + B(2)*12!*a^12/2!/12!
これを一般化すると、s=a+b*i として、
Σ_[n=4, n=n+2] 1/b^(n-3) * Σ_[r=0, r=r+2] B(n-r)*(n-2)!*a^r/(n-r)!/r!
(注 B(0)は計算しないので、B(2)まで計算するか、B(0)=0 と理解するかしてください。)
注 (-1)^n を付ける必要がある。
式だけを見ると複雑そうですが、並べて書いてみると、とても綺麗な構造になっています。これをプログラム化して計算させるのは難しくありません。(mq003.java)
これにより、kv(s)の完全公式の目鼻が付きました。しかし、e^f_θ(s) にはベルヌーイ数が含まれるので、途中までしか収束しません。式としては完全イクオールなのですが、それは理論上と言うことでしかありません。とは言うものの、誤差はわずかであり、bが増えると誤差は減少するので、実際上は問題ありません。
試しにこの式を使った計算と、先の近似式の計算とどのくらい違うかを確認してみます。
a=0.5 のときが -1/12b + 13/720b^3 - 37/20160b^5 + . . . であり、これが角度の近似公式ですが、b=2 のとき -3.946707589E-02 です。完全公式では n=16 まで計算すると -3.9455469E-02となります。誤差無しの答えは -3.945596491E-02 なので、誤差も目に付きますが、b=10にすると、目に付くところに誤差はありません。ましてや、bがある程度大きくなると、近似公式でも何も問題はありません。ましてや、完全公式をやです。
■ 結論
あとは、kv_θ(0.5+b*i) の他の公式とe^f_θ(s)を合計すると、以下のようになります。
kv_θ(0.5+b*i) = e^f_θ(0.5+b*i) - b*ln(2pi*e) + f01_θ(0.5+b*i) + f04_θ(0.5+b*i)
これだと分かり難いのですが、近似公式を詳しくしただけなので、近似公式を参考にしてください。
e^f_θ(0.5+b*i) = Σ_[n=4, n=n+2] 1/b^(n-3) * Σ_[r=0, r=r+2] B(n-r)*(n-2)!*(0.5)^r/(n-r)!/r!
ln(2pi*e)=2.837877067
f01_θ(0.5+b*i) = b*ln(b) + Σ_[r=2,r=r+2] -(-1)^(r/2)/2^r/r/b^(r-1)
e^(b*pi)=P とすると、
f04_θ(0.5+b*i) = -pi/4 + Σ_[r=1,r=r+1] (-1)^(r+1)/(2r-1)/P^(2r-1)
となります。
式が完成したのでプログラム化して計算可能となります。ただし、ベルヌーイ数が含まれるので、計算誤差 (注 いわゆる誤差ではなく、ベルヌーイ数特有の現象です。) には気を付けなければなりません。
■ kv(s)の極座標分析(その2の補足)
(updated 18/01/03)
「kv(s)のその2」は判りにくいので、その前にもっと判りやすい綺麗な公式を紹介しておきます。
極座標というより角度公式のほうが判りやすいのではないでしょうか。a=0.5を一般化して、すべてのaに対して角度公式を明らかにしたのが「その2」ですが、a=0のとき、a=0.5よりきれいな式になっています。これは取り上げる価値があります。
公式を挙げておきます。a=0のときですが、a=1も同じです。
kv_th(0+b*i) = b*ln(b) - b*ln(2*pi*e) - pi/4 - 1/12b - 1/360b^3 - 1/1260b^5 - 1/1680b^7 - . . .
これをベルヌーイ数で表すと、b*ln(b) - b*ln(2*pi*e) - pi/4 - B(2)/(1*2)/b + B(4)/(3*4)/b^3 - B(6)/(5*6)/b^5 + B(8)/(7*8)/b^7 - . . . と、きれいに並びます。
特に説明はいらないようなので、これで終わりです。a=-1 でも、a=-2 でも、有理数表現ができることはお判りいただけると思います。その法則について説明しているのが「その2」です。
■ kv(s)の極座標分析(その2)
a=0.5 の場合については、完全公式が見つかりました。その研究過程で a=0.5 以外の場合でも公式化が可能かもしれないと思いつきました。以下はその観点から分析した結果です。角度公式は見つかりましたが、長さ(絶対値)の公式はまだ未完成です。今後、さらなる分析により長さの公式も発見したいと願っています。ここでは角度公式を紹介します。
先の説明と重複するところがありますが、再度、初めから説明して見ることにします。
kv(s)=k(1-s)/k(s) が kv(s) の定義です。kv(s) = s! *2*cos(pi*s/2) / { s*(2*pi)^s } という公式はリーマン仮説証明で非常に重要な役割を果たしています。それゆえ、これをさらに分析することにします。
s! = (s/e)^s * √(2pi*s) * e^mo(s) これは実数階乗の公式を複素数になおしたものですが、bがプラスのときに成り立ちます。(s/e)^sの分母を全体の分母に移します。すると、kv(s) = s^s * √(2pi*s) * e^mo(s) * 2cos(pi*s/2) / { s * (2pi*e)^s } となります。
s=a+b*i とすると s^s = s^a * (cos(b*ln(s))+i*sin(b*ln(s))) なので、
kv(s) = s^a * (cos(b*ln(s))+i*sin(b*ln(s))) * √(2pi*s) * e^mo(s) * 2cos(pi*s/2) / { s * (2pi*e)^s } となります。
右辺が複雑になったので、いくつかに分割して分析します。
f01(s) = s^a * √(2pi*s) / s
f02(s) = cos(b*ln(s))+i*sin(b*ln(s))
f03(s) = e^mo(s)
f04(s) = 2cos(pi*s/2)
f05(s) = (2pi*e)^s
と名付けておきます。kv(s) = f01(s) * f02(s) * f03(s) * f04(s) / f05(s) ということです。
■ f01(s) = s^a * √(2pi*s) / s
s^a=(a+b*i)^a です。(a+b*i)を極座標表示に直すと √(a^2+b^2)*(cos(θ)+i*sin(θ)) となります。θ=atan(b/a) です。
ですから、(a+b*i)^aの極座標表示は (a^2+b^2)^(a/2) * (cos(θ*a)+i*sin(θ*a)) となります。
√(2pi*s) / s = √(2pi/s) 、√(2pi)は別にしておき、1/√(s) の √s の極座標を計算します。すると、(a^2+b^2)^0.25 * (cos(θ/2) + i* sin(θ/2)) となります。ゆえに、先の式を√sで割ると言うことなので、長さ(絶対値)は割り算と√(2pi)、角度は引き算となります。結果は、
f01_abs(s) = √(2pi)*(a^2+b^2)^(a/2-1/4) f01_θ(s) = atan(b/a)*(a-1/2) です。
■ f02(s) = cos(b*ln(s))+i*sin(b*ln(s))
f02(s)_abs(s) の式の極座標絶対値公式は近似値まで求めたが、まだ完全公式には至っていません。
a=0.5 のとき √e * e^(-pa*b) * { 1 - 1/24b^2 + 41/4750b^4 - ...
a=1 のとき e*e^(-pi/2)*{ 1 - 1/3/b^2 + 23/90/b^4 - 1223/5670/b^6 + ...
a=2 のとき e^2*e^(-pi/2)*{ 1 - 8/3/b^2 + 896/90/b^4 - 218368/5670/b^6 +
この一般形を求めてみたところ、
f02_abs(s) = e^a/e^(pa*b) * { 1 - a^3/3b^2 + a^5*(5a+18)/90b^4 - a^7*(35a^2+378a+810)/5670b^6
bが小さいときは以下の式を使います。
f02_abs(s) = 1-b^2/a + b^4/2a^2 - b^4(b2-2)/6a^3 + b^6(b^2-8)/24a^4 - b^6(b^4-20b2+24)/120a^5 + b^8(b^4-40b^2+184)/6!a^6 . . .
詳しくは後日また説明します。
角度公式は a=0.5のとき、b*ln(b) + 1/8/b - 1/64/b^3 + 1/384/b^5 - ... であることはすでに紹介してあります。aが一般のとき、
f02_θ(s) = b*ln(b) + a^2/2b - a^4/4b^3 + a^6/6b^5 - a^8/8b^7 + ....
と、綺麗に並びます。
つまり、f02_θ(s) = b*ln(b) + Σ_[r=2,r=r+2] a^r/r/b^(r-1) です。
aが大きいところでは、f02_θ(s) = b*ln(a) + b^3/2a^2 - b^5/4a^4 + b^7/6a^6 - b^9/8a^8 + .... となります。
■ f03(s) = e^mo(s)
mo(s)=B(2)/2s + B(4)/12s^3 + B(6)/30s^5 + B(8)/56s^7 + . . . と定義されています。
つまり、mo(s) = Σ_[r=2,r=r+2] B(r)/r(r-1)/s^(r-1)
e^mo(s) = 1 + 1/12n + 1/288n^2 + . . . ということで、スターリングの公式に登場する式になります。
e^mo(s)の極座標絶対値は、まだ綺麗に纏まらないので、ここでは角度だけを説明します。
すでに、a=0.5の完全角度公式のときに説明してありますが、e^mo(s)の角度は以下の式で計算できます。
f03_θ(s) = Σ_[n=2, n=n+2] { (-1)^(n/2)/b^(n-1) * Σ_[r=2, r=r+2] B(r)*(n-2)!*a^(n-r)/(n-r)!/r! }
判りやすく書くと、
f03_θ(s) = - 1/b * { B(2)*0!*a^0/0!/2! }
+ 1/b^3 * { B(2)*2!*a^2/2!/2! + B(4)*2!*a^0/0!/4! }
- 1/b^5 * { B(2)*4!*a^4/4!/2! + B(4)*4!*a^2/2!/4! + B(6)*4!*a^0/0!/6! }
+ 1/b^7 * { B(2)*6!*a^6/6!/2! + B(4)*6!*a^4/4!/4! + B(6)*6!*a^2/2!/6! + B(8)*6!*a^0/0!/8! }
以下略
注 a=0 のときは、0^0 および、0/0 が発生して、上記の式は成り立ちません。aがマイナスのときも、まだ未完成のようです。
■ f04(s) = 2cos(pi*s/2)
f04(s)の絶対値公式は、あまり綺麗でないのですが、実部公式と虚部公式から計算することができます。pa=pi/2
f04_re(s) ≡ e^(b*pa)*cos(a*pa) * { 1 + 1/e^(b*pi)}
f04_im(s) ≡ e^(pi/2*b)*sin(a*pa) * { - 1 + 1/e^(b*pi) }
すると、絶対値は f04_abs = √( f03_re(s)^2 + f03_im(s)^2 ) で計算できます。
角度は、同じ発想で、次の式になります。
f04_θ(s) は atan(f04_im(s)/f04_re(s))
■ f05(s) = (2pi*e)^s
f05_abs(s) = (2pi*e)^a = 17.079468^a (注 bに係わらず同じ式)
f05_θ(s) = b*ln(2pi*e) (注 aに係わらず同じ式)
■ 結論
kv(s) = f01(s) * f02(s) * f03(s) * f04(s) / f05(s) なので、絶対値については、掛け合わせて、角度は足し合わせて、合計を計算します。
絶対値はまだ未完成なので、ここでは角度だけを説明します。
角度は足し算になるので、 kv_θ(s) = f01_θ(s) + f02_θ(s) + f03_θ(s) + f04_θ(s) - f05_θ(s) となります。
f01_θ(s) = atan(b/a)*(a-1/2)
f02_θ(s) = b*ln(b) + a^2/2b - a^4/4b^3 + a^6/6b^5 - a^8/8b^7 + ....
f03_θ(s) = Σ_[n=2, n=n+2] { 1/b^(n-1) * Σ_[r=2, r=r+2] B(r)*(n-2)!*a^(n-r)/(n-r)!/r! }
f04_θ(s) = atan(f04_im(s)/f04_re(s)) で計算します。
f04_re(s) ≡ e^(b*pa)*cos(a*pa) * { 1/e^(b*pi) + 1 }
f04_im(s) ≡ e^(b*pa)*sin(a*pa) * { 1/e^(b*pi) - 1 }
f05_θ(s) = b*ln(2pi*e)
kv004.java、mp004.java で計算。
この中で bが小さいと収束しないところもありますが、角度の完全公式であることには変わりありません。これにより、kv(s)の角度がどうなるか、bがある程度大きなところでの姿が明らかになります。
表紙に戻る 前のページへ 次のページへ
|