リーマン証明から派生した公式

　　　　　　　　　　　　　　　　　　　　　　　　　　　　(update 09/09/22)


■　　　　　　x!*(-x)!



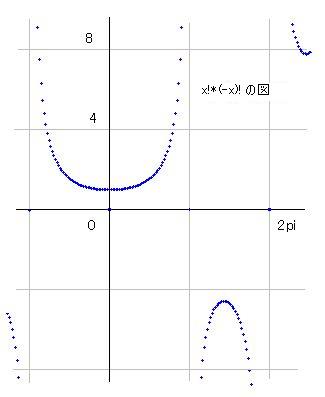x!*(-x)!も綺麗な式で表現できます。マイナス階乗公式を使って整理すると　 x*pi/sin(x*pi)　となります。x=0　付近の式を f(x) とし、係数を a(2), a(4), のように表示すると、以下のようになります。

f(x) = 1 + a(2)*x^2 + a(4)*x^4 + a(6)*x^6 + . . .

a(2) = 1.644934067, 　a(4) = 1.8940656, 　a(6) = 1.9711021, . . .

a(2) = pi^2/6, 　a(4) = pi^4*7/360, 　a(6) = pi^6*31/15120, . . .

これを眺めていて気が付いたのですが、a(2) = k(2) です。ですから、k(r)と何らかの関係があるかも知れないと思って、a(r)を k(r)で表現してみました。すると、a(4) = k(4)*7/4,　 a(6) = k(6)*31/16,　となりました。つまり、a(r) = k(r)*(2^(r-1)-1)/2^(r-2)　ということです。符号を無視すると、k(r) = pi^r*B(r)*2^(r-1)/r!　であることは判っているので、a(r) = pi^r*B(r)*2*(2^(r-1)-1)/r!　となります。

これは推測に基づく結論ですが、ためしに r=8　として計算してみましょう。k(8)*127/64 = 1.992466003　となります。そこで、実際に計算してみたところ、a(8) = 1.992466　となりました。検証終わり。

これで、a(10)も、a(12)も計算できることになります。つまり、a(10) = pi^10*B(10)*2*(2^9-1)/10!　ということで、B(10) = 5/66　なので、a(10) = 1.998079015　となります。

a(12) = 1.99951537, 　a(14) = 1.999878341, 　a(16) = 1.999969529, 　どうも２に近づくようですが、そうすると、ここにもひとつ公式が見つかったことになります。

r→∞で、2 = pi^r*B(r)*2*(2^(r-1)-1)/r!　なので、B(r) = r!/pi^r/(2^(r-1)-1)　となります。





■　　　　　　B(x)、k(x) の別公式


B(x)はいろいろな式で計算できますが、k(x)のベルヌーイ数表示を逆にすると、B(x) = -k(x)*x!/pi^x/2^(x-1)　となります。B(x)=-k(1-x)*x　というのもあります。今回、x*pi/sin(x*pi) 　の分析からまた新しい計算式を発見しました。r→∞で、2 = pi^r*B(r)*2*(2^(r-1)-1)/r!　となるので、これを　B(x) = x!/pi^x/(2^(x-1)-1) * f(x) と置いて、この f(x) を確定してみようと考えました。すると、驚くほど綺麗な式が現れました。このf(x)をlt(x)と名前を付けておきます。

lt(x) = 1 - 1/2^x + 1/3^x - 1/4^x + 1/5^x - . . .

すると、B(x) = lt(x)*x!/pi^x/(2^(x-1)-1)　と書くことが出来ます。ただし、これは符号や奇数を無視して計算した結果でしたので、再度符号を考慮して検討したところ、-cos(x*pi/2)を加えて、B(x) = - lt(x)*x!*cos(x*pi/2)/pi^x/(2^(x-1)-1)　を導くことが出来ました。xが大きいときは速やかに収束してくれます。これは近似値ではないので、使えるのではないでしょうか。

たとえば、これを　k(x)=-B(1-x)/(1-x)　に代入します。マイナス階乗公式も使って整理すると、k(x) = lt(1-x)*(2pi)^x*cos((1-x)*pi/2)/(x-1)!/(2^x-1)/sin(x*pi)　となります。cos((1-x)*pi/2)/sin(x*pi)　は　1/2cos(x*pi/2) なので、
k(x) = lt(1-x)*(2pi)^x/(x-1)!/(1-2^x)/2cos(x*pi/2)　となります。xがマイナスのとき収束します。

k(x)=lt(x)*2*cos(pi*(1-x)/2)*cos(pi*x/2)/sin(pi*(1-x))/(1-2^(1-x))　と書くことも出来ます。cos(pi*(1-x)/2)*cos(pi*x/2)/sin(pi*(1-x)=1/2　なので、
k(x)=lt(x)/(1-2^(1-x))　となります。xがプラスなら収束するので、これで複素数も計算できます。





■　　　　　　lt(x) = 1 - 1/2^x + 1/3^x - 1/4^x + . . . を分析



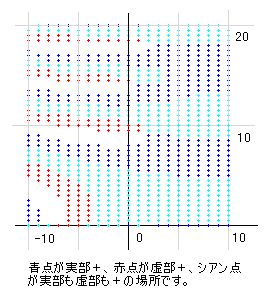
lt(x)は　k(x)と形が似ているだけでなく、B(x)を介して繋がっているので、同じ場所に零点を持つことが予想されます。さっそくこの零点図を作ろうと思ったのですが、計算するのに時間がかかるので、今回は作業を端折って、簡略な図を作成しました。これでもだいたいの所は判ります。

k(s)の零点がlt(s)でも零点になっているように見えます。ただ、k(s)で零点でないところまでもlt(s)では零点になっているみたいなので、これについては検討が必要です。どこかが間違っているかもしれません。

一応、このまま分析すると、lt(x)とk(x)は対応しているので、lt(x)を速やかに収束させる式を求めることが出来ます。k(x)のときと同様に計算すると、以下の式を求めることが出来ます。

lt(x,r) = 1 - 1/2/x^r + r/4/x^(r+1) - r(r+1)(r+2)/2/4!/x^(r+3) + . . . 　となるので、ここで登場する係数をlet(r)/2/r!と理解しておきます。また、C(n,r)=n!/(n-r)!/r!　なので、かけ算部分をC(n,r)で置き換えます。

lt(x,r) = 1 - let(1)*C((r-1),1)/2/(r-1)/x^r + let(2)*C(r,2)/2/(r-1)/x^(r+1) - let(4)*C((r+2),4)/2/(r-1)/x^(r+3) + let(6)*C((r+4),6)/2/(r-1)/x^(r+5) -

lt(x,r) = 1 - 1/2/x^r + Σ_[p=1,∞] let(2p)*C((1-2+2p),p)/2/(r-1)/x^(r-1+p)
となります。

かえって分かりにくく表示されてしまったかもしれませんが、このように表記できることはとても面白いことです。ただし、この式を用いてさっそく計算してみたところ、どういうわけか収束しないので、実際上の価値はありませんでした。

let(r)は次のように並ぶ数列です。

let(1)=-1, let(2)=1, let(4)=-1, let(6)=3, let(8)=-17, let(10)=155, let(12)=-2073, let(14)=38227　. . .

このlet(r)をかなり大きな所まで計算してみて気が付きましたが、隣同士を割るとpi^2*r　にきわめて近い数になっています。それで、r→∞で　let(r) = 4*r!/pi^r　であることが判りました。

近似値では困るので、ここでも let(r) = f(x)*4*r!/pi^r　と置いて、f(x)を求めたところ、1 + 1/3^r + 1/5^r + 1/7^r + . . . 　という綺麗な式になりました。 (^^)　　そこで、これにも名前を付けることにして、lu(r)　としておきます。lu(r) = Σ_[p=1,∞] 1/(2p-1) 　ということです。これを使うと let(r) の値を速やかに計算することが可能となります。

lu(r)の計算には特に困ったことはなかったのですが、形の上から、これもスピード計算できる別の式があるのではないかと思い、検討したところ、以下の式が見つかりました。この式については、一部おかしな所があり、いまだ研究途上なのですが、面白い点が見つかったので公表しておきたいと思います。

rはxに表記変えしておきます。

lu(x) = lu(x,r) + 1/r^(x-1) - 1/2/r^x + x/6/r^(x+1) - x(x+1)(x+2)/90/r^(x+3) + x(x+1)(x+2)(x+3)(x+4)/945/r^(x+5) - . . .

これに現れる係数をlot(r)と名付けておくと、lot(0)=1, lot(1)=-2, lot(2)=6, lot(4)=-90, lot(6)=945, lot(8)=9450, lot(10)=93555, . . . 　となります。これ以上の計算は時間がかかるのと、誤差も大きくなるので、諦めかけたのですが、ふと見ると、この数が k(r) の計算に登場する数と同じことに気が付きました。

k(2)=pi^2/6, k(4)=pi^4/90, k(6)=pi^6/945, k(8)=pi^8/9450, . . .であることはすでに計算されています。同じ並び方なので、計算しにくかった lot(12) もこれで確定させることが出来ます。つまり、k(12)=pi^12*691/638512875　なので、lot(12)=638512875/691 　となるはずです。計算してみると、見事一致しています。ここに登場する級数は互いに関連するものばかりであるのに驚かされます。

lot(r) = pi^r/k(r)　

これはとても綺麗ではないでしょうか。

lot(r)と k(r)が関連しているなら、B(r)とも関連していることになります。　k(r) = B(r)*pi^r*2^(r-1)/r!　なので、これを代入すると、なんとpiが消えてしまいました。　lot(r) = r!/B(r)/2^(r-1)

これだけ関連があるならlet(r)とも関連しているかもしれないと思って眺めていると、let(12) = -2073 = -691*3　であることに気が付きました。B(12)=-691/2730 なので、let(12)/B(12)=8190　となり、整数化するだけでなく、マイナスまで消えてしまいました。let(r)/B(r)を調べたところ、すべて整数化し、マイナスもなくなります。これは面白いと思い、さらに検討したところ、なんと　let(r)/B(r)=2*(2^r-1)　となっているではありませんか。　ヽ(゜Д゜)ノ !! 　偶然にしてはできすぎていますね。

さて、さらに整理すると、lu(x)-k(x) = - 1/2^x - 1/4^x - 1/6^x - . . . . なので、lu(x)-k(x) = -1/2^x*k(x)　となり、lu(x)=k(x)(1-1/2^x)=(2^x-1)/2^x*k(x)　となります。k(x)=lu(x)*2^x/(2^x-1)　でもあります。lt(x)-lu(x) = - 1/2^x*k(x)　なので、lt(x)=lu(x)-1/2^x*k(x)　から、lt(x) = k(x)*(2^x-2)/2^x　という式を導けます。これは検算によっても正しいと認められます。こちらの式の方が先の式より計算が簡単です。

まとめると、


lu(x) = (2^x-1)/2^x * k(x)

lt(x) = (2^x-2)/2^x * k(x)

ということです。

lu(x) = 1 + 1/3^x + 1/5^x + 1/7^x + 1/9^x + . . . .　ですが、この零線図が右図です。

lt(s)とよく似ていて、k(s)と同じ場所に零点を見つけることが出来ます。ただし、この図の中にもk(s)と異なる場所に別の零点が発生しています。これはおそらく　(2^x-1)/2^x　から来た零点なのでしょう。

なお、lt(1) = ln(2) = 0.69314718　です。綺麗な数字になりますね。

1 - 1/3 + 1/5 - 1/7 + 1/9 - . . . = 0.7853981634 = pi/4　となります。






■　　　　　　kd(x) = 2^x/(2^x-1) * 3^x/(3^x-1) * 4^x/(4^x-1) * . . .　の分析


kd(x)はゼータ関数のオイラー積表示に似ていますが、素数列ではなく、２からの自然数列に変更してあります。こちらの方が数列としては自然なので、これがどのような関数になるか疑問になりました。そこで、まずはk(x)と同じ形に変更し、さらには、ゼータ関数からk(x)を求めたやり方で、このkd(x)が速やかに収束するような式を求めてみたいと思います。

kd(x) = 1 + (1/2)^x + (1/3)^x + 2*(1/4)^x + (1/5)^x + 2*(1/6)^x + (1/7)^x . . .

係数が２のときと、３のときもあり、単純な法則ではなさそうです。係数をp(r)の数列と理解すると、p(2)=1, p(3)=1, p(4)=2, p(5)=1, . . . 　と並びます。何も付かないときがあります。さらに先まで並べてみます。

+ 3*(1/8)^x + 2*(1/9)^x + 2*(1/10)^x + (1/11)^x + 4*(1/12)^x + (1/13)^x + 2*(1/14)^x

このくらい並べてみると、ある程度の法則が見えてきます。素数はすべて１です。6=2*3 のように、ふたつの素数の積は２です。では、なぜ１２は４なのでしょうか？　

以下、係数だけを並べてみます。１０区切りとして、１から並べたのが次の表です。

1, 1, 1, 2, 1, 2, 1, 3, 2, 2, 　　　1, 4, 1, 2, 2, 5, 1, 4, 1, 4
2, 2, 1, 7, 2, 2, 3, 4, 1, 5,　　　1, 7, 2, 2, 2, 9, 1, 2, 2, 7,
1, 5, 1, 4, 4, 2, 1, 12, 2, 4,　　　2, 4, 1, 7, 2, 7, 2, 2, 1, 11
1, 2, 4, 11, 2, 5, 1, 4, 2, 5,　　　 1, 16, ???

これを見て法則が判る人はいますか？

法則があることは間違いありません。しかし、どういう法則なのか？　次の係数を確信を持って言うにはまだ早い感じです。もっと先まで計算しなければなりません。しかし、この先を計算するにはひどく時間が掛かります。このあたりで何とか結論を出したい気分ですね。

素数同士のかけ算は２です。４＊素数は４です。８は３ですが、８＊素数は７です。１６は５で、１６＊素数は１２です。３２は７で、６４は１１、かなり不規則ですね。

素数が３つある数は２＊３＊５＝３０のような数ですが、係数は５です。２＊３＊７＝４２の係数は５。
　
素数が４つの数は２＊３＊５＊７＝２１０で、まだ計算できていません。

４＊素数２つは４＊３＊５＝６０ですが、係数は１１。　では、４＊素数３つは？


いろいろ考えて、ようやく法則が判りました。

たとえば、1/12 のとき、１２に注目してこれを素因数分解し、12=2^2*3 とします。12の因数になりうるのは、1, 2, 3, 4, 6, 12 の６つです。まずは、１を除いて、２の列に１と２の倍数を書いておきます。１，２，４，８，１６と並びます。このうち１２以上の数は関係ないので消しておきます。３の列は、１，３，９，と並びます。４の列は、１，４　です。６の列は、１，６　となり、１２の列は、１，１２　です。

まず、２の列から検討し、２列内の数字と、それより下位の数字を掛け合わせて１２になるものを探します。２の列には下位がないので、次に３の列を見ます。ここで、３の列の３と２の列の４を選ぶと、３＊４で１２になります。これでひとつ数えます。次に４の列を見ます。すると、４＊３＊１があります。これで２個目、次に６の列を見ます。すると、６＊１＊１＊２があるので、合計３個、１２の列を見ると、１２＊１＊１＊１＊１で、合計４個となります。答えは４で正解です。

１８の場合は、１＊１８，２＊９，３＊６，６＊３，９＊２，１８＊１で、２の列には１８はありません。３列と２列の数を掛けて１８になるのは、９＊２で１個、６列では、６＊３＊１で合計２個、あとは、９＊１＊１＊１で３個、１８＊１，１，１，１で４個、合計４個です。正解は４個

２４でやってみます。１＊２４，２＊１２，３＊８，４＊６，６＊４，８＊３，１２＊２，２４＊１です。
２列ではなし、３列では、３＊８で１個、４列では、４＊３＊２で合計２個、６列では、６＊４＊１＊１で合計３個、８列では合計４個、１２列と２４列で合計６個となります。正解は７個、ひとつ足りません。６＊１＊１＊４が抜けていました。それで合計７個となります。６＊１＊１＊４と６＊４＊１＊１が区別されるところが重要です。

３２では、２列で３２自身がありで、合計１個、４の列では、４＊８、１６＊２で合計３個、８列では、８＊４＊１と８＊１＊４で、合計５個、１６列では１６＊１＊１＊２で、合計６個、３２＊１＊１＊１＊１で、合計７個となります。

これをプログラム化すれば何とか計算できるはずですが、どうプログラム化させるか、現在検討中です。このプログラム化が出来たとしても、k(s)と異なり、基準となる確定値がないので、速やかに収束させる式を導出できるかどうか、あまり自信がありません。ならば解析接続で求められるのでは？という気にもなりましたが、まだ勉強していません。

一応、kd(x)のまま計算することにしたところ、ｘが１に近いとなかなか収束してくれず、もしかすると発散するのではとの予想も立ててみましたが、発散する証拠はなく、むしろ収束する状況証拠はいくつか見つかりました。


なお、kd(x)の中で唯一確定値になるのは　kd(2)です。　kd(2)=2 となるのは注目すべきことです。

参考までに kd(x)のATN図を載せておきます。kd(1.5)=5.68..., kd(1.3)=25.0???　ですが、これを図にすると、傾きがやや緩くなっているように見えます。とすると、この青線はやはり　(1,∞)　に繋がっているのでしょう。









■　　　　　　kd(x) の続き


k(x)の零点図が描けたので、kd(x)の零点図も描けるのではないかと思いつきました。k(x)と同様の方法で収束式を見つけ、それを複素数化すれば良いはずなので、計算してみたところ、綺麗な収束式になりませんでした。式の全体を把握するためには法則を見つけなければなりません。ところが、kd(x)の場合、今のところこれと言った法則が見つかりません。これでは近似式で終わってしまい、零点を求める式になりません。

一応、途中までの式を公表しておきます。この式からだれか法則を見つけてくれる人はいないでしょうか。

kd(x,n) = 2^x/(2^x-1) * 3^x/(3^x-1) * 4^x/(4^x-1) * . . . * n^x/(n^x-1)　とします。

kd(x) = kd(x,∞) ということです。

kd(x,n))/kd(x)=lz0(x,n)+lz1(x,n)+lz2(x,n)+lz3(x,n)+.....　と表記することにします。

lz0(x,n) = 1 - 1/(x-1)/n^(x-1) + 1/2/n^x - B(2)*x/2!/n^(x+1) - B(4)*x(x+1)(x+2)/4!/n^(x+3) - . . . .　となります。これはk(x)を計算するときに登場する式と同じなので法則があり、計算可能です。

lz1(x,n) = 1/2/(x-1)^2/n^(x+1)
lz2(x,n) = -(3x-2)/(2x-1)(2x-2)/n^(x+2)

lz3(x,n) = (11x-13)/24/(x-1)/n^(x+3)

lz4(x,n) = -x/8/n^(x+4)

lz5(x,n) = x(x-4)(3x+1)/(x-1)/1440/n^(x+5)

lz6(x,n) = x(x+1)(3x+2)/480/n^(x+6)

lz7(x,n) = -x(x+1)(x+2)(5x^2-21x-24)/12/7!/(x-1)/n^(x+7)


以上の式を見て、lz8(x,n)を予想できるでしょうか。lz9(x,n)はどうなるでしょうか。そもそもプラスとマイナスの現れ方が不規則です。また、分母に(x-1)が交互に現れているという点では法則があるとも言えますが、通常の法則とはかなり異なります。しかも、この先にさらに別種の式が付加されるらしいという予想も出てきたので、このあたりで諦めることにしました。

しかし、これは近似値であることは間違いないので、x→∞でかなり正確な値を得ることが出来ます。



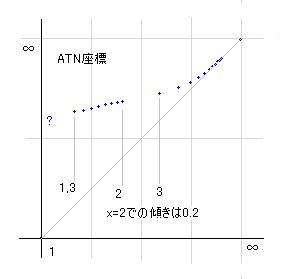
問題は、これがx→1　で成り立たないと言うことです。それでは意味がないので、何とかx→1 でも成り立つ式はないものかと探したところ、kd(x) = (f(x)/x)^(1/(x-1))　という式を得ました。このf(x)は、まだ式としては未確定ですが、ATN座標で表すと右図のようになります。

この図の x→∞ のf(x)が傾き0.5に近づくのは明らかですが、x→1 においてどうなるかは容易に判定できません。3の近傍に収束しそうと見えますが、どうなのでしょうか。一応 3として計算したところ、綺麗なf(x)式を得られませんでした。また、3.14　としても綺麗になるわけではなく、収束するという確証は得られませんでした。むしろ、→０になる可能性もあるという結論です。kd(x)の分析は一筋縄ではいきません。






■　　　　　　リーマン零点の現れ方の分析


a=0.5上の実部線・虚部線が零点で交差するところがリーマン零点です。kv(s)=k(1-s)/k(s)とすると、kv(s)のサイクルごとに必ずひとつ発生します。それは虚部線の上りのときですが、そこを通る実部線は、上りのときもあり、下りのときもあります。上りと下りが交互に現れるわけではなく、何らかの法則があるようにも見え、また無さそうにも見えます。そこで、そのどちらが正しいかを明らかにするために、以下のような分析をしてみました。

実部線が下りのときに零点が発生する場合を１とし、上りのときに発生する場合を０とします。最小の実部リーマン零点は１４．１３４ですが、このときの実部線は下りなので１となります。次のリーマン零点は２１．０２２で上りですから０となります。こういう具合に順番に調べて、その数字を並べると以下のようになります。最後の２はプログラムにとって終わりの印で、便宜上、７つごとに区切っておきました。

実際にプログラム化して計算した結果は次のとおりです。

0,1010100,1011001,0111011,0001001,0001101,0100010,0101001,1010110,0111000,0011100, 2

これを２進数少数と見立てて、１０進数に変換したところ、0.661695.... となりました。この数が循環小数なら法則があると言うことで、もし無理数なら法則がないことになります。


＜追加　2015/12/22＞

上記の　1,0, の並びは、線の上り・下りだけでなく、リーマン零点がkv(s)の実零線に対して、上にずれるか、下にずれるかとも関係しています。また、もし、この並び方が確定するなら、リーマン零点はすべて a=0.5 上に存在することになります。なぜなら、リーマン零点がa=0.5上になければ、1,0 が並ばなくなり、k(s)の虚零線はkv(s)の実零線とz=0で交差して、上にも下にもずれない点が発生します。つまり、1とも、0とも判定できない現象が生じると言うことです。これでは困ります。

もし、上記の数が存在するなら、リーマン零点はすべてa=0.5上にあるということであり、a=0.5上にないリーマン零点が存在するなら、上記の数も存在しなくなります。これは証明ということではありませんが、面白い現象ではないでしょうか。


なお、これと関連しますが、pj(s)という関数の虚零線はkv(s)の虚零点とほとんど同じ場所を通過します。しかし、必ずわずかにずれています。そのズレ方を二進数として解釈することが出来ます。



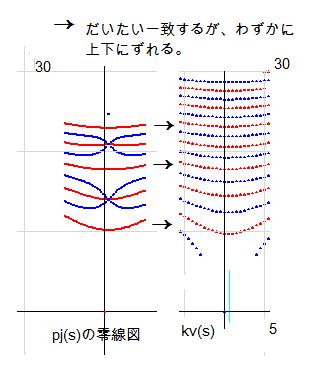
pj(s)とは　pj(s) = k(s) * k(1-s) と定義される関数です。a=0.5で虚部はすべて零となります。しかし、虚零線はa=0.5を通過していて、その場所はkv(s)の虚零点の近くです。上にきたときを１とし、下にきたときを０とします。どちらにずれるかを調べてみると、1,1,0,1,0,0,1,0,1,1と並びます。上記の数とは一致しませんが、この数もまた１０進数に変換することが可能です。また、リーマン零点がa=0.5上にないと成り立たない数となっています。

二進数を 0.1101001011... として１０進数に直すと　0.823... あたりになります。












■　　　　　　円周率を二進法で表わすと

なお、前期の二進法を円周率と比較するために、円周率の二進法表示を計算してみました。すると、以下のようになっていました。

11 . 0010010 0001111 1101101 0101000 1000100 0010110 1000110 0001000 1101001 1000100 1100011 0011000

pi/2 は　1.5707963　ですが、二進法表示では　　　1 . 1001001 0000111 1110110 1010100 0100010 0001011 0100011 0000100 0110100 1100010 0110001 1001100 0101000 1011100 0000011

面白いというか・・・、pi と　pi/2　の二進法表示はひとつ右にずれただけのことですね。当たり前ですが、実際に並んでいる数字を見ると、なるほどという思いがします。

（pa001.javaで計算）







■　　　　　　マイナス階乗公式の問題点
　　　　　　　　　　　　　　　　　　　　　＜追加　　2010/05/20＞

問題はなかったので、この章は削除しました。＜削除　　2010/07/30＞