派生した証明

　　　　　　　　　　　　　　　　　　　　　　　　　　　(updated 19/04/17)


■　　　　　　p3=2 、k_p3(s)　の場合


k_p3(s)については、すでに　hirokuroのリーマン証明ver60　の中で説明してありますが、それを再掲しておきます。

k_p3(s)は　k(s)の部分関数です。p3は計算深度（精度）をあらわす数字ですが、この深度を変数としてとらえたものがk_p3(s)となります。

具体的には、k(s) = lim_[n→∞] { zt(s,n) + ber(s,n) }　というk(s)の式を分解して、nまで計算した式を p3=n と考えます。zt(s,p3) = 1 + 1/2^s + 1/3^s + ... + 1/p3^s ということです。ber(s,n)は無限式なので、これも有限な式に変更します。

ber(s,n) = Σ_[r=0,∞] B(r)*(s-2+r)!/r!/(s-1)!/n^(s-1)/n^r

ber(s,n)の rは無限大に増加する数ですが、これを有限の範囲で止めたときを p3　とします。nをp3としたときのp3とは別の数ですが、どちらも任意の数なので、便宜上、同じと考えることにします。つまり、k_p3(s) = zt(s,p3) + ber(s,p3) 、かつ r=p3 ということです。ver60では、p3を実数に拡大して分析しましたが、ここではその必要がないので、当初の定義に戻って、自然数として考えます。

そして、p3=2　としたのが、今回、ここで取り上げる関数になります。つまり、

k_2(s) = 1 + 1/2^s　 +　 1/(s-1)/2^(s-1) - 1/2/2^s + s/12/2^(s+1)

という関数です。


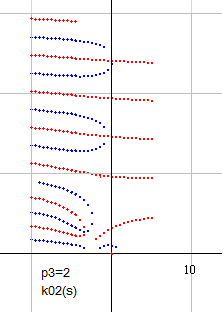
この関数の零線図は右のようになります。


右無限大は、１以外の項では、分母にある s が巨大になるので、すべて０になります。残るのは１だけなので、右無限大はすべて (1,0) になります。実零線は右無限大に到達できないので、必ず横Ｕ字形を作ります。すると、その間を走っている虚零線と交わり、そこに零点が発生します。

その零点の場所は a=0.5 付近のように見えますが、計算上、b=33 より上では、a=0.5軸より右に来ています。

s=0.5+i*b　を代入して、a=0.5上の式を導くと以下のようになります。

2^(0.5+b*i) = 2^0.5 * { cos(b*ln(2)) + i*sin(b*ln(2)) } 　なので、　1/2^(0.5+b*i) = { cos(b*ln(2)) - i*sin(b*ln(2)) } / 2^0.5 　となります。 A=cos(b*ln(2)) , B=sin(b*ln(2)) としておきます。すると、1/2^(0.5+b*i) = (A-i*B) / 2^0.5 　となります。

1/(1-s) = 1/(0.5-b*i) = (0.5+b*i)/(0.5^2+b^2) です。　C=0.5^2+b^2 としておきます。代入して整理すると、

k_2(0.5+b*i) = 1 + (A-i*B)/2^0.5 + (0.5+b*i)*(A-i*B)*2^0.5/C - (A-i*B)/2/2^0.5 + (A-i*B)*(0.5+b*i)/12/2^1.5

実部は　　　1+A/2^0.5+(0.5*A+B*b)*2^0.5/C - A/2/2^0.5 + (0.5A+B*b)/12/2^1.5

虚部は　　　-B/2^0.5 + (-0.5*B+b*A)*2^0.5/C + B/2/2^0.5 +(A*b-0.5B)/12/2^1.5

となります。

実部を　Ａ　について整理すると　　　A*{ 1/2^0.5+0.5*2^0.5/C-1/2/2^0.5+0.5/12/2^1.5 } 　。　Ｂ　について整理すると　　　B*b{ 2^0.5/C+1/12/2^1.5 } 　となります。

bが増大しても、A, B　は +-1 の範囲内に留まり、1/C　は ０ に近づきます。つまり、実部の増加要因は　B*b だけとなります。

虚部は　b*A*2^0.5/C+A*b/12/2^1.5　が増加要因ですが、b/Cは互いに打ち消しあって、増加しません。ですから、A*b/12/2^1.5 だけが増加要因となります。

b の増加とともに、実部・虚部ともに　b*sin(b*ln(2))、　b*cos(b*ln(s))　に近い形で増加するので、a=0.5上では、実部零点、虚部零点は交互となり、マイナス部分は必ず増大するので、実零線と虚零線の交点は必ずa=0.5の右側になります。

以上で証明終わり。（・・・　と言いたいところですが、これは暫定の証明です。　）





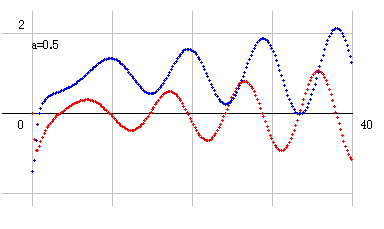
a=0.5のyz図を見ると良くわかります。

右図はb=0から40までの図です。青線がマイナスになるのが33付近であることが確認できます。


この証明は一見正しそう・・・というより、正しいかもしれません。しかし、問題がなきにしもあらずです。これについては確信がないので、まだ検討中ですが、ひとつの疑問は、「零線図の零点がa=0.5の右側にあることの証明のためには、a=0.5の波が必ず大きくなることだけでは不充分ではないか」ということです。これについては説明が難しいので、図を載せておきます。



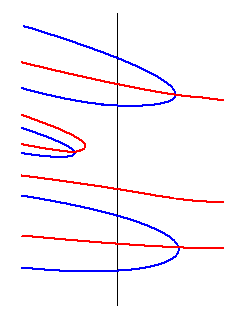
右図において、真ん中の実部横Ｕ字形はa=0.5を超えていません。しかし、a=0.5上の波は通常通りです。先の証明には右図のようにならないという証明が欠けています。ゆえに、先の証明は失敗と言うことになります。

もっとも、先の証明に付け加えるなら、完全に正しい証明が可能になるかもしれません。今のところ、その証明を思いつかないので、ペンディングになっています。

ただ、ここで、興味深く、また重要だと思うのは、同じ問題（困難さ）がリーマン証明の中にもあるということです。リーマン証明において、a=0.5上の角度公式が見つかっています。ですから、a=0.5上の波のリズムは確定します。そのリズム変化から「仮定上の零点が存在しない」と言いたいところです。しかし、リズムを乱すことなく仮定上の零点が存在してしまう可能性はまだ残っています。この「まだ残っている」可能性を否定するのが大変で、リーマン証明がなかなか完成しないことになります。

p3=2　の証明が成功するなら、そのやり方をリーマン証明で使えるかもしれません。

（注　　　hirokuroのリーマン証明ver70では、p3=2 の証明を使うことなく、別のやり方で証明が成功しました。しかし、それはそれとして、p3=2 の場合の証明は研究する価値があると思います。）





■　　　　　　輪にならないことの証明


微分係数が一致する複素関数では、実零線、虚零線は輪になることは出来ません。その証明をここでしておきます。

この証明をリーマン証明の中でしないことの理由は、リーマン証明（ver70）として必要な証明ではないからです。リーマン証明で使うのは、実零線と虚零線が作る閉鎖空間が発生しないことであって、実零線、虚零線が単独で輪になるケースを分析する必要がありません。しかし、輪にならないことも事実なので、その証明もまた興味深いと考えて、ここでトライすることにしました。

単独で輪になると、零点がないので、その零線上の極座標角度はすべて同じになります。実零線ならば、pi/2 か 3pi/2 です。虚零線なら　0 か pi です。実零線の場合を取り上げると、その上下の頂点をaについての実部微分零線が通ります。左右の頂点を虚部部分零線が通ります。

上の頂点の実部は零ですが、虚部には０以外の値があります。その値の虚部等高線がその点を通っています。すると、その等高線はその点以外のどこかで必ず実零線と交わります。

実零線と虚部等高線が作る閉鎖空間は、実零線、虚零線の作る閉鎖空間と同じ矛盾を発生させます。なぜなら、等高線の高さをhとすると、k(s)=c+d*i を変形させて c+(d-h)*i の零線図を描きます。すると、先の等高線が零線になり、実零線と虚零線の閉鎖空間が発生し、矛盾が生じます。ですから、先の実零線と虚部等高線の閉鎖空間も発生しないことになります。

c+(d-h)*i の関数が微分係数一致であることは、計算上確認できます。この計算上ということが証明として許されないとするなら、上記の証明は成り立ちません。今のところ、k(s)が微分係数一致関数であることも計算によって確認できるだけであり、その他、普通の関数すべてが微分係数一致関数なのも計算上ということで、証明されているわけではありません。証明が必要なことなのでしょうか。今のところ、上記の証明で終わりにしておきます。





■　　　　　　微分係数一致関数の証明


証明が必要かもしれないと思ったので、証明に挑戦してみることにしました。

同一関数内で、微分係数一致の部分と一致しない部分がある関数は存在しないという証明です。

そこで、仮定法により、まずは存在したと仮定します。すると、一致部分と一致しない部分の区別が可能になり、一致部分と一致しない部分の境界線が発生します。一致した部分ではa方向の実部微分とb方向の虚部微分が一致し、aの実部微分零線と bの虚部微分零線が同じ線となって走っています。ところが、一致しない部分ではこのふたつの線が別々の線として存在しています。すると、一致部分から一致しない部分へと変わる境界線において、一致部分から来た微分零線が一致しない部分に抜けるとき、ふたつの微分零線に分かれることになります。ひとつの線がふたつの線に分かれるということは矛盾ですから、最初の仮定が成り立たないことを示しています。

以上、証明終わり。