実数値での階乗計算方法

■　　　　　　階乗の公式


普通、n!は正の整数で定義されていて、n!=n*(n-1)*(n-2)* .... *3*2*1 として計算します。しかし、これだと 2.3 とか、10.5のときなど計算できません。ところが階乗の公式を使うと、小数であっても計算可能となります。

n! = (n/e)^n * √(2*pi*n) * e^( 1/12n - 1/360n^3 + 1/1260n^5 ... .)
つまり、
n! = (n/e)^n * √(2*pi*n) * e^ ｛ su(2)/n + su(4)*2/n^3 + su(6)*4!/n^5 + su(8)*6!/n^7 .... ｝
もしくは、
n! = (n/e)^n * √(2*pi*n) * e^ ｛ B(2)/2n + B(4)/12n^3 + B(6)/30n^5 + B(8)/56n^7 .... ｝
となります。

ただ、この式には少し問題が残っています。su(n)にしろ、ベルヌーイ数にしろ、振動・発散するので、式全体も振動して近似値しか得られません。そこで、ひとつの工夫が必要になります。nが大きいと振動の影響も減少するので、n!を計算するとき、まず(n+10)!とか、(n+100)!を計算し、それを用いてn!を求めます。

たとえば、n=3.6 として、 (n+10)! として計算する手順を示しておきます。
n+10=13.6 ですから、n=13.6 を階乗の公式に代入します。そして、B(10)くらいまで計算すると、その結果、n!=3.00776726+10^10 あたりになるはずです。そこで、13.6!/13.6/12.6/11.6/.... 5.6/4.6=13.38128587093.... を得ることが出来ます。さらに精度を上げたいときは、必要に応じて、(n+100)!などにすれば良いということです。

-1<n<0 の時でも計算は可能です。マイナスのままでは虚数になってしまいますが、n+10として、プラスの数にした上で、(n+10), (n+9)... と割ってゆきます。たとえば、(-0.5)!を求めたいときは、n+10=9.5ですから、これを階乗の公式に代入し、その上で、8755649.016/9.5/8.5/7.5/.... 1.5/0.5=1.7724538509... を得ることが出来ます。これが√pi であることは知られているので、プログラムの適否を調べる手段として使うことが出来ます。



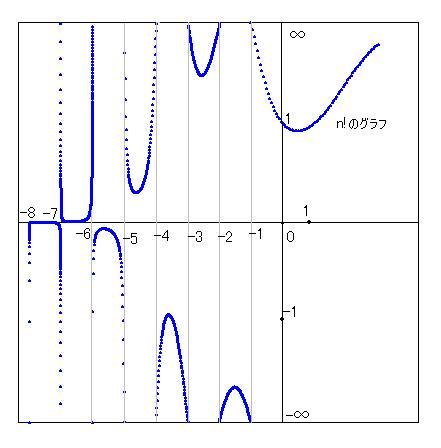
n<-1 の時も階乗計算は可能です。その結果を右図に示しておきました。n=-1, n=-2 などの時は無限となりますが、それ以外では有限の値を取ります。（このグラフの縦軸はATN座標となっています。）

また、別ページでも示しておきましたが、(-n)! = n*pi/n!sin(n*pi) という公式を発見しました。これにより、n!から(-n)!を計算することができます。

高等数学の世界では、なぜか階乗よりもガンマ関数のほうがポピュラーです。ガンマ関数は、Γ(n) = (n-1)! という式になり、階乗と基本的には同じなのですが、これを階乗の公式に代入すると、Γ(n) = (n/e)^(n-1)*√(2*pi*n)*f(n) という形になり、あまり綺麗とは言えなくなります。f(n)のところは、面倒なので、まだ確定させていませんが、この式の形からしても、ガンマ関数よりも階乗の方が基本形であると認定することが出来ます。

式の形から判断するのは、su(n)とB(n)の関係も同じです。su(r) = sin(pi*r/2-pi/2) * 2/(2*pi)^r * { 1+(1/2)^r+(1/3)^r+'(1/4)^r+.... 　} と B(r) = sin(pi*r/2-pi/2) * 2/(2*pi)^r * r! * { 1+(1/2)^r+(1/3)^r+'(1/4)^r+.... 　} を比べると、B(r)の方にr! が付加されています。つまりその分だけB(n)が余分であり、su(n)の方がより本質的公式であることを示しています。また、この場合のB(1)=1/2 という結果は、最初のB(n)の定義に反しています。これも問題です。

まぁ、それはそれとして、階乗を微積分を使わなくても説明できると言うことは、高校生でも理解できるレベルになったということです。今後は、この階乗の公式を高校数学でも取り上げていただけたらと思っています。



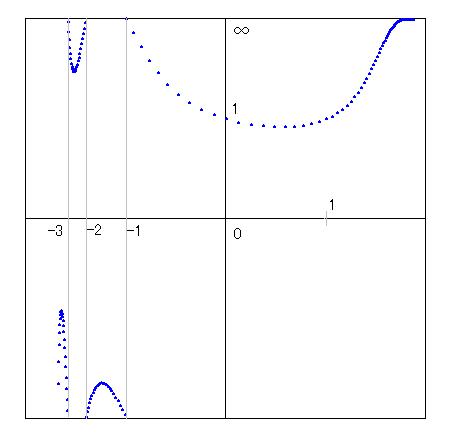
x! の全体図も重要なので掲載しておきます。ATN座標にすると、全体を図示することができます。x=-1が無限大で、x=0, x=1 が１，x=∞が無限大になります。xが-2, -3, -4, ... のときは +-∞となりますが、その間は値を持ちます。

マイナスの階乗、逆数の階乗の公式

ｘがマイナスでも上記の実数値計算の方法で値を求められます。ただマイナス階乗の公式もあるので、それをここで再度説明しておきます。この公式は第１２の広場を書くときに発見したもので、とても綺麗な形をしています。x! から (-x)! を直接計算できるので大きなマイナスを計算する場合には必要になるでしょう。

(-x)! = x*pi / x!sin(x*pi)

これがマイナス階乗の公式です。たとえば、x=2.5 を代入するとそのまま -2.5 の階乗が計算できます。学校ではー１以下の階乗については習わないのではないでしょうか。それほど難しくない内容なので、この程度は常識にしてもらいたいものです。

(-2.5)!=2.3632718012...

xがマイナスの整数のところではすべて +-∞ となります。上記のgraph31.jpgのグラフがとても判りやすいですね。ATN座標の重要性も高校レベルで認識されるべきではないでしょうか。

この図を見ながら思ったのですが、これを1/yにするとマイナス部分もひとつの線となるのではないでしょうか。さっそく 1/x! の図を描いてみました。


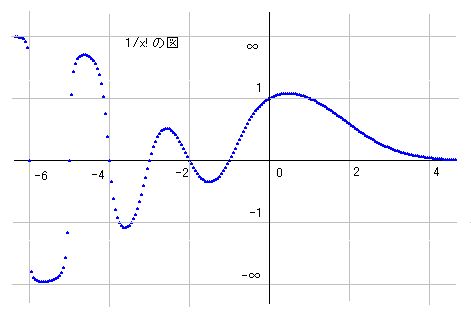
予想通りの綺麗な曲線を得られました。縦軸はATN座標 atan(y) となっています。xが増加すると限りなく零に近づき、マイナス方向ではマイナス整数ごとに零となり、より左に行くほど大きく波打ちます。幸いにもATN図なので無限大も図の中に収まります。　

x!図の無限点は1/x!ではすべて零になるので繋がります。マイナスの公式にsinが登場するので、この図もsin曲線を基本としていることが判ります。

式として表記すると以下のようになります。n! とよく似ているのは、当然なのかもしれませんが、とても面白い現象だと思います。

1/n! = (e/n)^n * e^( - 1/12n + 1/360n^3 - 1/1260n^5 + ... .) / √(2*pi*n)


e^( 1/12n - 1/360n^3 + 1/1260n^5 - . . . = 1 + 1/12n + 1/288n^2 - 139/51840n^3 - 571/2488320n^4 + 163879/209018880n^5 + . . . 　であるのに対し、以下の式の右辺までが似ているのは偶然でしょうか。

e^( - 1/12n + 1/360n^3 - 1/1260n^5 + . . . = 1 - 1/12n +1/288n^2 + 139/51840n^3 - 571/2488320n^4 -163879/209018880n^5n^5 . . . .　となっています。



さて、(1/x)! はどのような式になるのでしょうか。これについてはいろいろな計算をしている途中で見つけたのですが、とても綺麗な形になっていますのでご紹介します。

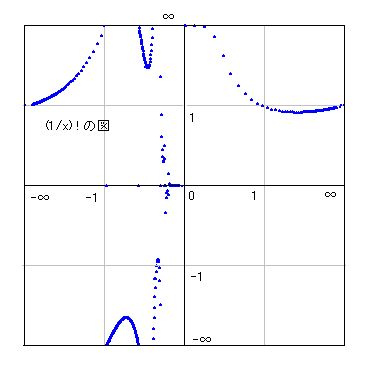
図を描くと右のようになります。縦軸も横軸もATN座標です。

k(2)=1.64493406, k(3)=1.202056902, k(4)=1.082323234, k(5)=1.03692775514, k(6)=1.017343062, k(7)=1.00834927738, . . . とします。
e=2.718281828, eu=0.577215664 とします。そして (1/x)! = e^f(x)　となるようにf(x)を定義します。すると、f(x)は以下のように表現できます。

f(x) = -eu/x + pi^2/12/x^2 - 0.400685/x^3 + 0.2705808/x^4 - 0.2073855/x^5

これを　k(r) で書き表すと、

f(x) = -eu/x + k(2)/2x^2 - k(3)/3x^3 + k(4)/4x^4 - k(5)/5x^5 + k(6)/6x^6 . . .　
と綺麗に並びます。

この式が成り立つのは絶対値が１以上のところです。マイナスでも絶対値が大きいと収束します。

e^f(x) ですから、対数化したほうが綺麗かもしれません。もちろん、この場合はマイナスではいけません。つまり、　log(1/x!)/log(ee) = f(x) となります。

現在の数学界には、k(r)とゼータ関数を混同して平気な人がたくさんいますが、こういう定義レベルでの混乱があるというのは未来の人々からは笑われてしまうでしょうね。・・・それはそれとして・・・、k(r)とは　従来通りの説明になりますが、１以上の実数では、Σ[x=1,∞] 1/x^r で定義される数です。つまり、k(r)=1+1/2^r+1/3^r+... ということです。これと階乗とは直接関係がないのですが、しかし、逆数の階乗の公式にk(r)が登場すると言うことは、どういうことでしょうか。とても面白いではありませんか。

k(3), k(5), k(7) などが無理数なので、計算は面倒ですが、|x|>1 において f(x)が理論上収束することは注目に値します。


それから、もうひとつ付記しておきたいのは　0.5!, 1.5!, 2.5! などの階乗についてです。公式というほどのことでもないし、当たり前のことなので、今まで書いておこうという気がしなかったのですが、意外と知られていないので、ここで説明しておきます。

(-0.5)! = √pi = 1.77245385,　0.5! = √pi/2 = 0.886226925　であることは良く知られています。　1.5! = 3*√pi/4 = 1.329340388　であることも知られているはずですが、知らない人もいるみたいです。同じく、2.5! = 15*√pi/8 = 3.32335097,　3.5! = 105*√pi/16,　4.5! = 945*√pi/32, . . .

(-1.5)! = -2*√pi, (-2.5)! = 4*√pi/3, (-3.5)! = -8*√pi/15, . . .

結局、nがプラスのとき、(n-0.5)! = (2n-1)*(2n-3)*....*3*1*√pi/2^n となり、マイナスのときは　(n-0.5)! = 2^(-n)*√pi/(2n+1)/(2n+3)/.../(-3)/(-1) となります。

これもけっこう綺麗です。数学者なら常識と言える公式のはずですが・・・どうでしょうか。





(09/08/19 追加)
上記の　(1/x)!=e^f(x)　の公式で、1/x　を x　に置き換えても公式が成り立つことに気が付きました。考えてみれば当たり前ですが、こちらの公式の方が重要でしょう。

x! = e^f(x)　として、

f(x) = -x*eu + x^2*k(2)/2 - x^3*k(3)/3 + x^4*k(4)/4 - x^5*k(5)/5 + x^6*k(6)/6 . . .　
となります。

これも階乗の公式で、xの絶対値が小さいときはこれで計算できます。ただし、k(3)などは無理数で、前もって計算しておかなければなりませんから、便利というわけではありません。






(22/04/12 追加)
■　　　　　　階乗の公式の部品を検討する


実数の階乗の公式は x が小さいと誤差が大きくなります。それで、(x+n)! という大きな数で計算し、その結果を　/(x+n)/(x+n-1)/(x+n-2)/... 　と順次割っていって誤差をなくすのですが、計算が面倒だという問題があります。

この面倒臭さを生じさせるのは　(x/e)^x*√(2pix)*e^f(x) という式の e^f(x) 部分にあります。ベルヌーイ数が巨大化するので、普通のやり方では収束しなくなるわけです。そこで、この部分を　e^mo(x) と名付けて分析・研究することにします。

e^mo(x) = e^( 1/12n - 1/360n^3 + 1/1260n^5 ... .)

もしくは

e^mo(x) = e^ ( B(2)/2n + B(4)/12n^3 + B(6)/30n^5 + B(8)/56n^7 .... )

ということです。


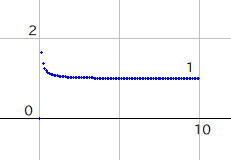
10より上はほとんど１なので、計算結果に大きな影響は与えません。






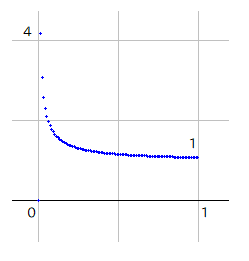１より小さい部分では値が増加していて、x=0 では無限大に近づくように見えます。

この無限大に近づく部分を式として表すと

e^mo(x) = 1/√(2pi*x) * { 1 - x*ln(x) + (1-eu)*x^2 - 72.055979...*x^3 + ..... }　という式が見つかります。この式では　72.055979... という有理数ではなさそうな数が現れるので、計算はこのくらいにしておきます。